Introduction à la Relativité (3ème partie)
- Vecteurs, formes linéaires et tenseurs
- Tenseur métrique
- Composantes covariantes et contravariantes
- Longueur d’une courbe
- Connexion de Levi-Civita
- Tenseur de courbure
- Gravitation et courbure
- Tenseur énergie-impulsion
- Equation d’Einstein
Vecteurs, formes linéaires et tenseurs
Dans la 2ème partie de cette série, nous avons posé les bases mathématiques de la relativité générale, en définissant les concepts de variété différentielle, de connexion, et de géodésique.
Avant de poursuivre, il faut maintenant introduire la notion de tenseur, que l’on va rencontrer à plusieurs reprises dans la suite. Le terme de “tenseur” peut faire peur à première vue, mais il n’y a en fait rien de compliqué !
Tout d’abord, on considère un espace vectoriel réel \(E\), c’est-à-dire un ensemble de vecteurs que l’on peut additionner entre eux et multiplier par un scalaire (un nombre réel), vérifiant un certain nombre de propriétés qu’on ne va pas détailler ici.
Si \(E\) est de dimension \(n\), tout vecteur \(u\in E\) peut se décomposer sur une base \((e_0, e_1, …, e_{n-1})\) sous la forme: \(u = u^\alpha e_\alpha\). On dit que les nombres \(u^\alpha\) sont les composantes contravariantes du vecteur, car si on multiplie les vecteurs de base par un certain facteur, les composantes varient d’un facteur inverse.
On appelle forme linéaire sur \(E\), ou covecteur, une application linéaire \(\omega\) de \(E\) dans \(\mathbb{R}\), c’est-à-dire telle que:
\[\forall (u,v)\in E^2, \forall \lambda\in \mathbb{R}, \omega(\lambda u + v) = \lambda \omega(u) + \omega(v)\]L’ensemble des formes linéaires sur \(E\) est appelé l’espace dual de \(E\), noté \(E^\ast\), qui est aussi un espace vectoriel de dimension \(n\). Si on appelle \(e^\alpha\) la forme linéaire qui à un vecteur \(u\) associe sa composante \(u^\alpha\) dans la base \((e_\alpha)\), alors la famille \((e^\alpha)\) forme une base de \(E^\ast\), appelée la base duale de la base \((e_\alpha)\). Une forme linéaire (un covecteur) \(\omega\) peut donc se décomposer sur cette base sous la forme: \(\omega=\omega_\alpha e^\alpha=\omega(e_\alpha)e^\alpha\). On dit cette fois que les nombres \(\omega_\alpha\) sont des composantes covariantes, car si on multiplie les vecteurs de base \(e_\alpha\) par un certain facteur, les composantes \(\omega_\alpha=\omega(e_\alpha)\) varient du même facteur.
On appelle tenseur d’ordre \((r, s)\) une forme multilinéaire sur \({E^\ast}^r\times E^s\), c’est-à-dire une application multinéaire (linéaire par rapport à chaque variable) \(T\) qui à \(r\) covecteurs de \(E^\ast\) et \(s\) vecteurs de \(E\) associe un nombre réel \(T(\omega_{(1)}, \omega_{(2)}, …, \omega_{(r)}, u_{(1)}, u_{(2)}, …, u_{(s)})\). On dit que \(T\) est \(r\) fois contravariant et \(s\) fois covariant.
Par exemple, un tenseur d’ordre \((0, 1)\) est tout simplement une forme linéaire (un covecteur) sur \(E\).
Autre exemple: un tenseur d’ordre \((1, 0)\) est une forme linéaire sur \(E^\ast\), c’est-à-dire une forme linéaire qui à une forme linéaire associe un nombre réel ! Si on considère un vecteur \(u\in E\), alors on peut définir une forme linéaire \(\tilde{u}\) de \(E^\ast\) dans \(\mathbb{R}\) qui à \(\omega\) associe le nombre \(\tilde{u}(\omega) = \omega(u)\). Réciproquement, on peut retrouver le vecteur \(u\) à partir de la forme linéaire \(\tilde{u}\), en posant \(u=\tilde{u}(e^\alpha)e_\alpha\). C’est pourquoi en pratique, on considère qu’un tenseur d’ordre \((1, 0)\) est équivalent à un vecteur de \(E\), même si en tout rigueur c’est un vecteur de l’espace \(E^{\ast\ast}\) (c’est-à-dire le dual de \(E^\ast\), appelé l’espace bidual de \(E\)).
Tout comme un vecteur ou un covecteur, un tenseur peut être représenté par ses composantes dans une certaine base. Si on considère par exemple un tenseur \(T\) d’ordre \((1, 2)\), on peut par linéarité écrire (toujours en utilisant la convention de sommation d’Einstein, qui montre ici toute son utilité):
\[\begin{align} T(\omega, u, v) &= T(\omega_\alpha e^\alpha, u^\mu e_\mu, v^\nu e_\nu) \\ &= T(e^\alpha, e_\mu, e_\nu) \omega_\alpha u^\mu v^\nu \\ &= T^\alpha_{\mu \nu} \omega_\alpha u^\mu v^\nu \\ \end{align}\]où les coefficients \(T^\alpha_{\mu \nu} = T(e^\alpha, e_\mu, e_\nu)\) sont appelés les composantes du tenseur \(T\) dans la base \((e_\alpha)\). Si \(E\) est de dimension 4 (comme l’espace-temps), ce tenseur a donc \(4^3 = 64\) composantes. On peut remarquer que par convention, les indices covariants d’une composante (ici \(\mu\) et \(\nu\)) sont toujours notés “en bas”, tandis que les indices contravariants (ici \(\alpha\)) sont notés “en haut”.
Une remarque qui sera utile pour la suite est qu’un tenseur d’ordre \((1, s)\) peut être vu comme une application s-linéaire de \(E^s\) dans \(E\), et réciproquement (de la même façon qu’un tenseur d’ordre \((1, 0)\) peut être vu comme un vecteur). Par exemple, on peut associer à une application bilinéaire \(\phi\) de \(E\times E\) dans \(E\) un tenseur \(\tilde{\phi}\) d’ordre \((1,2\)) défini par: \(\tilde{\phi}(\omega,u,v) = \omega(\phi(u, v))\). Réciproquement, à partir du tenseur \(\tilde{\phi}\) on peut construire l’application bilinéaire \(\phi\) définie par: \(\phi(u,v) = \tilde{\phi}(e^\alpha,u,v)e_\alpha\).
Tenseur métrique
Jusqu’ici, nous n’avons défini aucune notion de distance entre points de la variété, ni de longueur des vecteurs. La distance entre deux points dans une certaine carte ne donne a priori aucune information sur les points eux-mêmes dans la variété, puisque le choix d’une carte est complètement arbitraire. Il faut donc introduire une structure supplémentaire sur la variété, appelée le tenseur métrique, ou simplement la métrique, qui va permettre de définir des angles et des longueurs.
Comme nous l’avons déjà vu pour l’espace-temps de Minkowski, on appelle tenseur métrique (défini en un certain point \(p\)) une forme bilinéaire symétrique non dégénérée, c’est-à-dire un tenseur \(g\) d’ordre \((0, 2)\) qui à deux vecteurs tangents \(U\) et \(V\) de \(T_p M\) associe un nombre réel \(g(U,V)\), vérifiant les propriétés suivantes:
- \(g(U, V) = g(V, U)\) (symétrique)
- \((\forall V \in T_p M, g(U, V) = 0) \implies (U = 0)\) (non dégénérée)
Si on se place dans une certaine carte, on peut représenter les vecteurs par leur coordonnées dans la base \((e_\alpha) = \left(\frac{\partial}{\partial x^\alpha}\right)\), et on a donc:
\[\begin{align} g(U,V) &= g(U^\mu e_\mu, V^\nu e_\nu) \\ &= g(e_\mu, e_\nu) U^\mu V^\nu \\ &= g_{\mu \nu} U^\mu V^\nu \\ \end{align}\]où les coefficients \(g_{\mu \nu} = g(e_\mu, e_\nu)\) sont les composantes du tenseur métrique (dans la carte en question). Un point important est que même si les composantes de la métrique dépendent de la carte choisie, la métrique elle-même n’en dépend pas, car \(U\), \(V\) et \(g(U,V)\) sont définis indépendamment de toute carte.
La métrique est une généralisation du produit scalaire qu’on connait en géométrie euclidienne, et est sans doute le concept le plus important de la relativité générale. En effet à partir de la métrique, on pourra par exemple calculer les coefficients de la connexion (et donc la dérivée covariante), la courbure de l’espace-temps, la longueur d’une courbe, ou encore l’équation d’une géodésique. Notons qu’une métrique est une application définie en chaque point de la variété, mais par extension on appelle aussi métrique le champ de tenseurs qui à chaque point associe un tenseur métrique.
Tout comme en relativité restreinte, on peut définir la norme (plus exactement le carré de la pseudo-norme) d’un vecteur \(U\) à partir de la métrique:
\[g(U, U) = g_{\mu \nu} U^\mu U^\nu\]Un cas particulier de métrique est la métrique de Minkowski, que nous avons rencontrée en relativité restreinte (c’est la métrique d’un espace-temps plat, sans force de gravitation), définie par:
\[g(U, V) = U^0 V^0 - U^1 V^1 - U^2 V^2 - U^3 V^3\]Si on représente les composantes de cette métrique par une matrice, on a donc:
\[[g_{\mu \nu}] = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \\ \end{bmatrix}\]Composantes covariantes et contravariantes
Grâce au tenseur métrique, il est possible d’établir une correspondance (appelée isomorphisme canonique) entre un espace vectoriel \(E\) et son dual \(E^{\ast}\), autrement dit entre les vecteurs et les covecteurs.
Pour comprendre cette idée, on peut prendre l’exemple du produit scalaire usuel sur l’espace \(\mathbb{R}^2\), défini par \(\langle u, v \rangle = u^0 v^0 + u^1 v^1\). Si on se donne un vecteur \(u \in \mathbb{R}^2\), alors l’application \(\omega: v \longmapsto \langle u, v \rangle\) (c’est-à-dire l’application “produit scalaire avec le vecteur \(u\)”) est la forme linéaire (le covecteur) associée à \(u\), ayant pour coordonnées:
\[\omega_\alpha = \omega(e_{\alpha}) = \langle u, e_\alpha \rangle = u^{\alpha}\]Réciproquement, si on se donne une forme linéaire \(\omega\) sur \(\mathbb{R}^2\), alors on vérifie facilement que \(\omega(v) = \langle u, v \rangle\), avec \(u = \sum \omega(e_\alpha) e_\alpha\). On a donc bien une correspondance immédiate (dite canonique, car elle ne dépend pas de la base choisie) entre vecteurs et covecteurs de \(\mathbb{R}^2\), grâce au produit scalaire.
On peut généraliser cette idée à une variété munie d’une métrique \(g\). En effet, si on se donne un vecteur \(U \in T_p M\), on peut construire une forme linéaire \(\omega\) définie par:
\[\forall V \in T_p M, \omega(V) = g(U, V)\]\(\omega\) est un tenseur d’ordre \((0, 1)\), et on voit facilement que ses composantes dans une carte s’écrivent:
\[\omega_\alpha = g(U, e_\alpha) = g(U^\beta e_\beta, e_\alpha) = g_{\alpha\beta} U^\beta\]Puisque la forme linéaire \(\omega\) est associée canoniquement au vecteur \(U\), on la note également \(U\), mais il faut bien comprendre que c’est un abus de notation car on confond un vecteur avec un covecteur. Les coordonnées de \(U\), en tant que covecteur, sont donc:
\[U_\alpha = g_{\alpha\beta} U^\beta\]Le tenseur métrique \(g\) permet donc de transformer un vecteur en son covecteur associé, autrement dit de passer des coordonnées contravariantes \(U^\beta\) (du vecteur) aux coordonnées covariantes \(U_\alpha\) (du covecteur). On dit aussi que la métrique permet de “faire descendre” l’indice du vecteur, grâce à l’opération \(g_{\alpha\beta} U^\beta\) (appelée le produit contracté du tenseur \(g\) avec le vecteur \(U\)).
On peut également passer d’un covecteur au vecteur associé (c’est-à-dire “faire monter” l’indice) grâce à l’opération inverse:
\[U^\alpha = g^{\alpha\beta} U_\beta\]où \(g^{\alpha\beta}\) est le tenseur métrique inverse, obtenu en calculant l’inverse de la matrice \([g_{\alpha\beta}]\) (on peut en effet montrer que cette matrice est toujours inversible).
Longueur d’une courbe
On a vu qu’on ne peut en général pas relier deux points quelconques d’une variété par un vecteur, mais c’est tout de même possible lorsque ces points sont infiniments proches.
On considère une courbe \(\gamma\) et deux points \(p\) et \(q\) de \(\gamma\) tels que \(p=\gamma(0)\) et \(q=\gamma(d\lambda)\), où \(d\lambda\) est une variation infiniment petite du paramètre \(\lambda\). On peut alors définir le vecteur déplacement élémentaire \(dL\) du point \(p\) au point \(q\) par:
\[dL = \dot\gamma(0) d\lambda\]où \(\dot\gamma(0)\) est le vecteur tangent à la courbe au point \(p\).
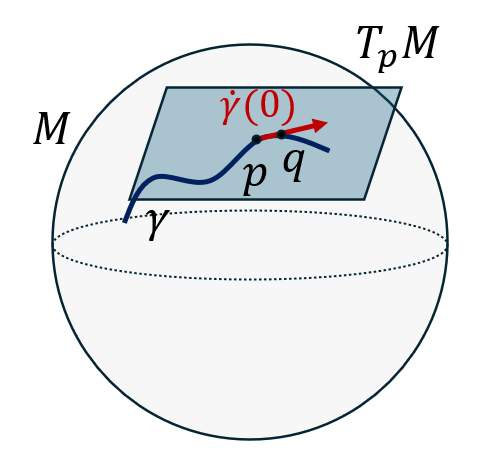
Cette définition est assez naturelle, par analogie avec le déplacement élémentaire d’un point mobile dans un espace affine euclidien: \(d\vec{r} = \vec{v} dt\). On peut montrer que l’action du vecteur \(dL\) sur un champ scalaire \(f\) est:
\[dL(f) = f(q) - f(p)\]On voit donc que \(dL\) ne dépend en fait que de \(p\) et \(q\) et est indépendant du choix de la courbe \(\gamma\) passant par \(p\) et \(q\).
Si on se place dans une certaine carte \(\phi\), on peut définir la variation infinitésimale \(dx^\alpha\) entre les coordonnées de \(p\) et celles de \(q\):
\[dx^\alpha = \phi(q) - \phi(p)\]On montre alors que \(dL = dx^\alpha \frac{\partial}{\partial x^\alpha}\), autrement dit les nombres \(dx^\alpha\) sont les coordonnées du vecteur \(dL\) dans la base des vecteurs tangents \( (\frac{\partial}{\partial x^\alpha})\).
On peut maintenant définir la longueur (intervalle) élémentaire \(ds^2\) de la courbe entre les points \(p\) et \(q\) à partir de la norme du vecteur déplacement élémentaire:
\[ds^2 = g(dL, dL)= g_{\mu\nu}dx^\mu dx^\nu\]Comme on a l’a vu en relativité restreinte, le signe de \(ds^2\) détermine le genre de l’intervalle élémentaire, et donc par extension de la courbe. Si \(ds^2>0\), l’intervalle est de genre temps, si \(ds^2<0\), l’intervalle est de genre espace, et si \(ds^2=0\), l’intervalle est de genre lumière.
Si on prend maintenant deux points quelconques \(p=\gamma(\lambda_0)\) et \(q=\gamma(\lambda_1)\) sur la courbe, alors la longueur \(L_\gamma(p, q)\) de la courbe entre ces points est simplement l’intégrale des longueurs élémentaires sur la trajectoire. Si on remarque que \(dx^\alpha = \dot{x}^\alpha d\lambda\), on a donc:
\[L_\gamma(p, q) = \int_{\lambda_0}^{\lambda_1}\sqrt{|g_{\mu\nu}\dot{x}^\mu \dot{x}^\nu|}d\lambda\]Dans le cas où la courbe est la ligne d’univers d’un observateur (c’est-à-dire sa trajectoire dans l’espace-temps), alors la longueur de la courbe entre deux points (c’est-à-dire deux événements) définit le temps propre de cet observateur.
Connexion de Levi-Civita
Pour rappel, on peut exprimer une connexion (ou dérivée covariante) \(\nabla\) en fonction de ses coefficients \(\Gamma_{\mu \nu}^\alpha\), mais sans information supplémentaire sur la variété il existe en fait une infinité de connexions possibles. Cependant, si on dispose aussi d’une métrique \(g\) sur la variété, alors on peut montrer qu’il existe une unique connexion compatible avec cette métrique, qu’on appelle la connexion de Levi-Civita.
Concrètement, cela signifie que si deux champs de vecteurs \(U\) et \(V\) sont transportés parallèlement le long d’une courbe \(\gamma\), alors leur “produit scalaire” \(g(U, V)\) est conservé par ce transport parallèle (on dit dans ce cas que la métrique est parallèle: \(\nabla g = 0\)). Une conséquence directe de cette définition est que le transport parallèle conserve les angles et les longueurs, exactement comme le ferait une translation dans un espace affine euclidien.
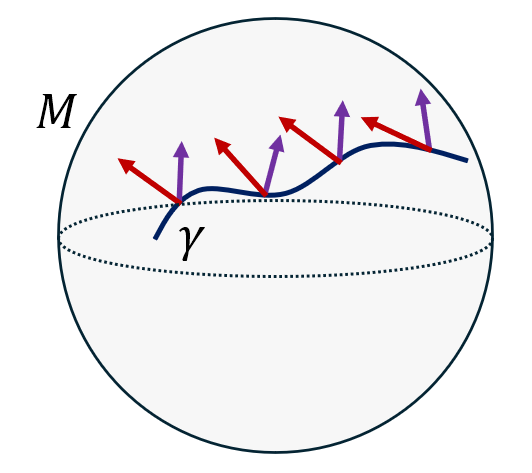
On peut montrer que les coefficients de la connexion de Levi-Civita, appelés les symboles de Christoffel, s’expriment en fonction des composantes de la métrique (et de son inverse) comme ceci:
\[\Gamma_{\mu\nu}^{\alpha}={\frac {1}{2}}g^{\alpha\beta}\left({\frac {\partial g_{\beta\mu}}{\partial x^{\nu}}}+{\frac {\partial g_{\beta\nu}}{\partial x^{\mu}}}-{\frac {\partial g_{\mu\nu}}{\partial x^{\beta}}}\right)\]Si on injecte cette expression dans l’équation des géodésiques vue précédemment (\(\ddot{x}^\alpha + \Gamma_{\mu \nu}^\alpha \dot{x}^\mu \dot{x}^\nu = 0\)), alors on peut montrer qu’une géodésique passant par deux points est une courbe de longueur extrémale entre ces deux points (de longueur minimale pour une courbe de genre espace, mais de longueur maximale pour une courbe de genre temps). Autrement dit, si on utilise la connexion de Levi-Civita, le chemin le plus court entre deux points est une ligne droite (au sens du transport parallèle).
Tenseur de courbure
Comme on l’a vu précédemment, le transport parallèle d’un vecteur d’un point à un autre de la variété dépend du trajet suivi. Ainsi, si on transporte parallèlement un vecteur (en vert sur le schéma ci-dessous) le long d’une petite courbe fermée, le vecteur obtenu après un tour complet de la boucle sera différent du vecteur de départ:
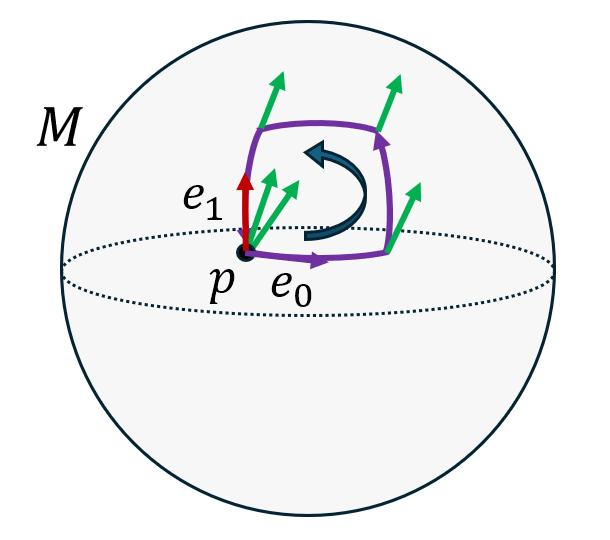
Sans rentrer dans les détails techniques, on peut montrer que la différence entre le vecteur de départ et celui d’arrivée peut être calculée à l’aide d’une application multilinéaire \(R\) sur l’espace des champs de vecteurs \(\Gamma(TM)\), définie par:
\[R(U, V, W) = \nabla_U(\nabla_V W) - \nabla_V(\nabla_U W) - \nabla_{[U, V]}W\]où \([U,V]\) est le commutateur des champs de vecteurs \(U\) et \(V\), qui est lui-même un champ de vecteurs défini par:
\[\forall f \in C^\infty(M), [U,V](f) = U(V(f)) - V(U(f))\]Comme on l’a vu, cette application multilinéaire \(R\) peut être considérée comme un tenseur d’ordre (\(1, 3\)), appelé le tenseur de courbure de Riemann.
Etant donnés trois champs de vecteurs \(U\), \(V\) et \(W\), le tenseur de courbure indique comment \(W\) varie selon qu’on le transporte parallèlement dans la direction \(V\) puis dans la direction \(U\), ou bien dans la direction \(U\) puis dans la direction \(V\).
Les composantes du tenseur de Riemann dans une carte peuvent s’exprimer en fonction des symboles de Christoffel (et donc de la métrique):
\[R^{\alpha }_{\mu \nu \kappa }={\partial \Gamma ^{\alpha }_{\mu \kappa } \over \partial x^{\nu }}-{\partial \Gamma ^{\alpha }_{\mu \nu } \over \partial x^{\kappa }}+\Gamma ^{\alpha }_{\nu \beta }\Gamma ^{\beta }_{\mu \kappa }-\Gamma ^{\alpha }_{\kappa \beta }\Gamma ^{\beta }_{\mu \nu }\]A partir du tenseur de Riemann, on peut former un tenseur d’ordre \((0, 2)\) appelé le tenseur de Ricci \(R_{\mu\nu}\), défini par:
\[R_{\mu\nu} = R^{\alpha}_{\mu\alpha\nu}\]On dit que le tenseur de Ricci est une contraction du tenseur de Riemann, car il est obtenu en faisant la somme de certaines composantes du tenseur de Riemann (celles pour lesquelles le premier indice est égale au troisième).
Enfin, en effectuant le produit contracté du tenseur métrique inverse avec le tenseur de Ricci, on obtient un champ scalaire \(R\) appelé courbure scalaire de Ricci, défini par:
\[R=g^{\mu\nu}R_{\mu\nu}\]Comme on va le voir prochainement, le tenseur de Ricci et la courbure scalaire sont à la base de l’équation d’Einstein, qui relie la courbure de l’espace-temps à la matière présente dans l’Univers.
Gravitation et courbure
Pour se faire une idée du raisonnement qui a conduit Einstein à découvrir son équation de la gravitation, nous allons prendre le cas simple d’un corps en chute libre à faible vitesse, dans un champ de gravitation faible, dans un référentiel galiléen.
Comme on l’a vu, l’accélération de ce corps est tout simplement égale au champ de gravitation:
\[\vec{a} = \vec{\mathcal{G}}\]Si on note les coordonnées du corps \(x^\alpha = (ct,x,y,z)\), cette équation s’écrit:
\[\begin{cases} \ddot{x}^0 &= 0 \\ \ddot{x}^i - \mathcal{G}^i &= 0 \text{ } (i=1,2,3) \end{cases}\]Si on remarque que \(\dot{x}^0 = c\), alors on peut mettre ces équations sous la forme suivante:
\[\ddot{x}^\alpha + \Gamma_{\mu \nu}^\alpha \dot{x}^\mu \dot{x}^\nu = 0\]avec \(\Gamma^i_{00} = -\frac{\mathcal{G}^i}{c^2} \) et tous les autres coefficients \(\Gamma_{\mu \nu}^\alpha\) nuls.
On retrouve donc exactement l’équation d’une géodésique dans un espace courbe, ce qui était précisément l’idée de départ de la relativité générale !
Si maintenant on cherche à calculer le tenseur de Ricci \(R^{\mu\nu}\) correspondant à cette courbure, on trouve que toutes ses composantes sont nulles, sauf la composante \(R^{00}\) (on dit la composante “temporelle-temporelle”, puisque \(0\) est l’indice correspondant à la coordonnée “temps”):
\[R^{00} = -\frac{1}{c^2}\frac{\partial \mathcal{G}^i}{\partial x^i}=-\frac{1}{c^2} \text{div} \vec{\mathcal{G}}\]Or on sait que la loi de la gravitation de Newton peut s’exprimer sous la forme suivante:
\[\text{div}\vec{\mathcal{G}}=-4\pi G \rho\]où \(\rho\) est la densité de masse (la masse volumique \(\frac{dm}{dV}\)) en chaque point de l’espace.
On obtient donc finalement:
\[R^{00} = \frac{4\pi G}{c^4}\rho c^2\]qui est une version simplifiée de l’équation d’Einstein, et montre que c’est l’énergie (\(\rho c^2\)) qui est à l’origine de la courbure de l’espace-temps (\(R^{00}\)). En effet, on sait que l’énergie d’un corps de masse \(m\) au repos est égale à \(E=m c^2\), et donc \(\rho c^2 = \frac{dE}{dV}\) est bien la densité d’énergie.
Cependant, cette équation ne peut pas être la “vraie” loi de la gravitation car la densité d’énergie \(\rho c^2\) dépend du référentiel choisi, or comme on l’a vu en relativité restreinte, les lois de la physique doivent pouvoir s’écrire indépendamment du référentiel. On sait par exemple que la vitesse dépend du référentiel, mais que la quadri-vitesse est, elle, définie de façon absolue dans l’espace-temps. Pour obtenir l’équation d’Einstein complète, il faut donc trouver un équivalent dans l’espace-temps de la densité d’énergie. Comme nous allons le voir, cet équivalent est un objet mathématique appelé le tenseur énergie-impulsion.
Tenseur énergie-impulsion
Pour fixer les idées, on va considérer un “nuage de poussière”, c’est-à-dire un ensemble de particules (toutes de masse \(m\), pour simplifier) se déplaçant toutes à la même vitesse.
On suppose que ce nuage est immobile dans un référentiel inertiel \(\mathcal{R}\), et que la densité d’énergie est \(\rho c^2\) en chaque point. Si maintenant on considère un référentiel \(\mathcal{R}’\) en mouvement rectiligne uniforme par rapport à \(\mathcal{R}\) à la vitesse \(u\), alors la transformation de Lorentz (voir la 1ère partie), montre que dans \(\mathcal{R}’\) la densité d’énergie devient \(\gamma^2 \rho c^2\), avec \(\gamma = \frac{1}{\sqrt{1-u^2/c^2}}\).
Sans rentrer dans la justification mathématique, ce facteur \(\gamma^2\) implique que la densité d’énergie doit être une composante d’un tenseur (symétrique) d’ordre 2: c’est le tenseur énergie-impulsion, noté \(T^{\mu\nu}\).
Pour comprendre ce qu’est le tenseur énergie-impulsion, il faut d’abord rappeler l’expression du quadrivecteur énergie-impulsion \(\mathbf{p}\) d’une particule de masse \(m\) et de vitesse \(\vec{v}\) dans un certain référentiel:
\[p^\alpha = (\gamma m c, \gamma m \vec{v}) = \left(\frac{E}{c}, \vec{p}\right)\]Pour mieux visualiser ce que sont les composantes du tenseur \(T^{\mu\nu}\), on va se placer pour simplifier dans un espace-temps à 3 dimensions (en ignorant la dimension \(z\)), mais l’explication se généralise facilement à 4 dimensions. Si on trace les lignes d’univers des particules du nuage dans un diagramme de Minkowski, on obtient quelque chose comme ceci:
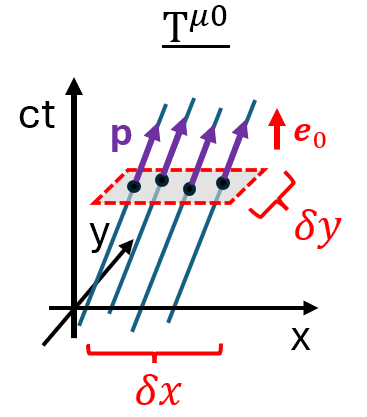
en supposant que le nuage se déplace dans la direction \(x\). Sur le schéma ci-dessus, on a representé l’intersection des lignes d’univers avec une petite surface de dimensions \(\delta x \times \delta y\), correspondant à une certaine valeur \(ct\) constante. Dans cet exemple, on voit quatre ligne d’univers traversant la surface, ce qui signifie qu’il y a quatre particules dans cet élément de surface.
La composante \(T^{\mu 0}\) du tenseur énergie-impulsion est alors définie comme la densité de la composante \(p^\mu\) du quadrivecteur énergie-impulsion \(\mathbf{p}\) sur la surface (en réalité dans un volume, si on se place dans un espace-temps à 4 dimensions), c’est-à-dire:
\[T^{\mu 0} = \frac{n c}{\delta x \delta y} p^\mu\]où \(n\) est le nombre de particules dans la surface (4 sur cet exemple). Le facteur “\(c\)” est nécessaire ici pour que le résultat soit cohérent avec les autres composantes du tenseur que l’on va voir ensuite.
Si maintenant on considère une surface de dimensions \(\delta y \times c\delta t\), correspondant à un certain \(x\) constant, on obtient le schéma suivant:
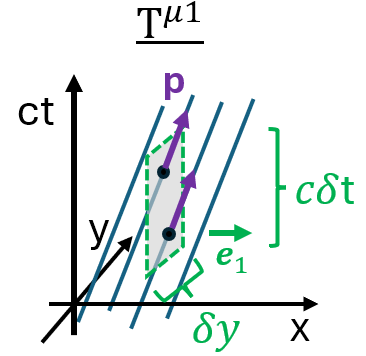
De la même façon, la composante \(T^{\mu 1}\) du tenseur énergie-impulsion est définie comme le flux de \(p^\mu\) à travers la surface, c’est-à-dire:
\[T^{\mu 1} = \frac{n}{\delta y \delta t} p^\mu\]où \(n\) est égal à 2 sur cet exemple.
Enfin, le flux de \(p^\mu\) à travers une surface définie par un \(y\) constant donne:
\[T^{\mu 2} = \frac{n}{\delta x \delta t} p^\mu\]Sur cet exemple, aucune ligne d’univers ne traverse cette surface, car la vitesse des particules dans la direction \(y\) est nulle, et donc les composantes \(T^{\mu 2}\) sont nulles également:
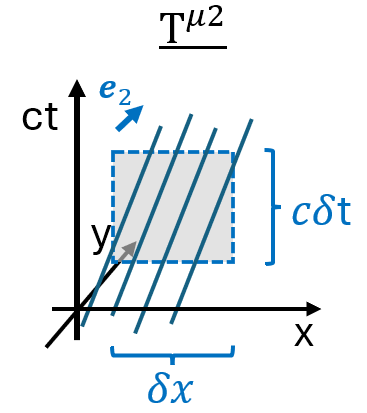
Plus généralement, les composantes du tenseur énergie-impulsion d’un nuage de poussière peuvent s’écrire sous la forme:
\[T^{\mu \nu} = \rho v^\mu v^\nu\]où \(\rho\) est la densité de masse au repos, et \(v^\alpha\) sont les composantes de la quadri-vitesse. Attention, \(v^\alpha\) contient déjà un facteur \(\gamma\), c’est pourquoi \(T^{\mu \nu}\) varie d’un facteur \(\gamma^2\).
En particulier, la composante temporelle-temporelle \(T^{00}\) dans un référentiel où le nuage est immobile vaut alors \( \rho c^2\), c’est-à-dire la densité d’énergie ! L’équation d’Einstein “simplifiée” vue précédemment peut donc tout simplement s’écrire:
\[R^{00} = \frac{4\pi G}{c^4}T^{00}\]Equation d’Einstein
D’après l’équation ci-dessus, on est tenté de croire que la loi de la gravitation de la relativité générale doit s’écrire:
\[R^{\mu\nu} = \frac{4\pi G}{c^4}T^{\mu\nu}\]en utilisant les tenseurs de Ricci et d’énergie-impulsion en entier, et pas seulement leur composante temporelle-temporelle.
En réalité, l’équation d’Einstein est légèrement plus complexe, et fait intervenir la courbure scalaire de Ricci \(R\) et le tenseur métrique:
\[R^{\mu\nu}-\frac{1}{2}R g^{\mu\nu} = \frac{8\pi G}{c^4}T^{\mu\nu}\]L’expression de gauche est appelée le tenseur d’Einstein, noté \(G^{\mu\nu}\), et l’équation d’Einstein peut donc s’écrire:
\[G^{\mu\nu} = \kappa T^{\mu\nu}\]où \(\kappa = \frac{8\pi G}{c^4}\) est simplement une constante qui permet de retrouver la loi bien connue de la gravitation de Newton, dans le cas où la courbure de l’espace-temps est très faible.
La raison pour laquelle il faut utiliser le tenseur d’Einstein \(G^{\mu\nu}\) au lieu du tenseur de Ricci \(R^{\mu\nu}\) est assez technique. Sans rentrer dans les détails, cela vient du fait que la divergence du tenseur énergie-impulsion est nulle (ce qui exprime le fait que l’énergie et la quantité de mouvement se conservent), et donc celle de \(G^{\mu\nu}\) doit l’être également. Il se trouve que la divergence du tenseur \(R^{\mu\nu}\) n’est pas nulle, mais en ajoutant le terme \(-\frac{1}{2}R g^{\mu\nu}\) on trouve bien un tenseur de divergence nulle. Ce point technique a d’ailleurs posé un gros problème à Einstein, qui a mis du temps à trouver la bonne équation !
Cette équation est extrêmement complexe, et il est impossible d’en calculer les solutions exactes sauf dans des cas très particuliers. Le cas le plus simple est celui d’un espace vide, la métrique obtenue étant alors celle de Minkowski, déjà rencontrée en relativité restreinte.
Un autre cas particulier important est celui de la courbure de l’espace-temps autour d’un corps sphérique de masse \(M\), tel qu’une étoile ou une planète. On obtient alors la métrique de Schwarzchild, qui peut s’écrire sous la forme suivante en coordonnées sphériques \((ct, r, \theta, \phi)\):
\[ds^2 = \left(1-\frac{R_s}{r}\right)c^2 dt^2 - \left(1-\frac{R_s}{r}\right)^{-1}dr^2 - r^2 d\theta^2 - (r \text{ sin }\theta)^2 d\phi^2\]où \(R_s=\frac{2GM}{c^2}\) est le rayon de Schwarzchild.
Lorsque le rayon d’une étoile est plus petit que le rayon de Schwarzchild, alors on voit que la composante \(g_{rr}\) du tenseur métrique tend vers l’infini quand \(r\) se rapproche de \(R_s\), et on obtient… un trou noir !