Introduction à la Relativité (1ère partie)
- Introduction
- Principe de relativité
- Transformation de Galilée
- Espace affine euclidien
- Le problème de la lumière
- Transformation de Lorentz
- Espace-temps de Minkowski
- Temps propre et dilatation du temps
- Diagramme de Minkowski et ligne d’univers
- Cône de lumière
- Composition des vitesses
- Quadrivitesse
- Dynamique relativiste
Introduction
La théorie de la relativité, élaborée par le célèbre Albert Einstein (entre autres) au début du XXe siècle, est avec la physique quantique un des piliers de la physique moderne. Tout le monde a déjà entendu parler de la formule \(E=mc^2\) et de l’espace-temps, mais il y a sans doute peu de monde qui soit familier avec les fibrés tangents, le tenseur de Ricci ou encore la connexion de Levi-Civita ! Et pour cause, bien que les principes fondamentaux de cette théorie soient assez simples à comprendre, pour bien en saisir toutes les subtilités il est nécessaire de maîtriser un certain nombre d’outils mathématiques plus ou moins avancés, ce qui peut être rapidement intimidant voire décourageant.
L’objectif de cette Introduction à la Relativité est de présenter les grandes lignes de la théorie de la relativité, restreinte puis générale, en introduisant progressivement les notions mathématiques nécessaires à la compréhension du sujet.
Bonne lecture !
Principe de relativité
Le principe de relativité a été découvert par Galilée au XVIIe siècle, et donc bien avant Einstein. Galilée avait résumé ce principe avec la formule suivante: “le mouvement est comme rien”, affirmation assez mystérieuse qu’il faut expliquer un peu. Galilée avait en effet remarqué que si on est enfermé dans un bateau ayant un mouvement rectiligne uniforme (c’est-à-dire se déplaçant en ligne droite à vitesse constante), il est impossible de se rendre compte que le bateau est en mouvement. Par exemple si on lâche un objet dans le bateau, il tombera à la verticale exactement comme si on était resté à quai. Du point de vue d’un observateur, être immobile sur terre ou immobile dans un bateau (en mouvement rectiligne uniforme) revient donc exactement au même, et d’ailleurs puisque la Terre tourne sur elle-même et autour du Soleil, personne n’est en réalité immobile ! C’est cette constatation qui est à la base du principe de relativité, qui en langage moderne s’énonce comme ceci:
Les lois de la physique sont invariantes par changement de référentiel inertiel
Pour comprendre ce principe, il faut déjà expliquer ce qui signifie un “référentiel inertiel”, aussi appelé référentiel galiléen.
De façon générale, un référentiel est défini par un solide (c’est-à-dire un ensemble de points fixes entre eux) auquel on rattache une coordonnée de temps et un système de coordonnées spatiales, constitué d’un point origine \(O\) et de 3 axes, fixes par rapport au solide de référence. On peut donc par exemple repérer un point \(M\) dans l’espace et le temps par un instant \(t\) et un vecteur \(\vec{r}=\vec{OM}\). Si on se place dans un repère cartésien \((O, \vec{e_x}, \vec{e_y}, \vec{e_z})\), alors on peut repérer le point par 4 coordonnées \((t, x, y, z)\). Il est à noter qu’on peut très bien changer de repère tout en restant dans le même référentiel, du moment que le repère est fixe par rapport au solide de référence. Une remarque importante pour la suite est que dans la physique de Galilée, le temps est absolu et ne dépend pas du référentiel choisi. On peut aussi choisir n’importe quel instant comme origine du temps (c’est-à-dire l’instant \(t=0\)), cela ne change absolument rien aux lois de la physique.
Un référentiel est dit inertiel (ou galiléen) s’il respecte le principe d’inertie, à savoir que dans ce référentiel tout objet qui n’est soumis à aucune force doit avoir un mouvement rectiligne uniforme. En particulier, un objet immobile dans un référentiel inertiel restera immobile s’il n’est soumis à aucune force. Le bateau dans l’exemple précédent est un référentiel inertiel, tout comme le quai (c’est-à-dire le référentiel terrestre).
La grande idée du principe de relativité est que tous les objets de l’espace sont en mouvement les uns par rapport aux autres, et qu’il n’existe aucun référentiel absolu. Par exemple, un passager est en mouvement par rapport au bateau, le bateau est en mouvement par rapport à la Terre, la Terre est en mouvement par rapport au Soleil, le Soleil est en mouvement dans la galaxie, etc. Par contre, ce que dit Galilée est que si on connait un certain référentiel inertiel \(\mathcal{R}\), alors tout autre référentiel \(\mathcal{R}’\) en mouvement de translation rectiligne uniforme par rapport à \(\mathcal{R}\) est aussi un référentiel inertiel. Par exemple, si le référentiel terrestre est inertiel, alors le référentiel du bateau l’est aussi. Une autre façon de le dire est que tous les référentiels inertiels sont équivalents, et qu’il n’existe donc pas de référentiel absolu ou privilégié.
Une petite remarque en passant: puisque la Terre tourne sur elle-même et autour du Soleil, le référentiel terrestre n’est en fait pas un référentiel inertiel. On peut considérer que ce référentiel est inertiel uniquement de façon approximative, à moins de faire intervenir des forces fictives dites d’inertie (force d’inertie d’entraînement et force de Coriolis). De façon générale, tout référentiel en mouvement accéléré (c’est-à-dire dont la vitesse varie en direction et/ou en norme) par rapport à un référentiel inertiel n’est lui-même pas inertiel. Ce n’est pas forcément intuitif, mais la rotation est un cas particulier d’accélération puisque la vitesse de chaque point varie en direction à chaque instant (excepté sur l’axe de rotation).
Pour en revenir au principe de relativité, il faut aussi préciser ce qu’on entend par “invariance par changement de référentiel”. Cela signifie que si on peut écrire une loi de la physique dans un référentiel inertiel donné, cette loi doit s’écrire de la même façon dans un autre référentiel inertiel. L’exemple le plus simple est la loi fondamentale de la dynamique (deuxième loi de Newton) bien connue:
\[m\vec{a} = \vec{f}\]où \(\vec{f}\) est la somme des forces s’exerçant sur un objet de masse \(m\), et \(\vec{a}\) son accélération dans un certain référentiel inertiel \(\mathcal{R}\).
On peut montrer que si on se place dans un autre référentiel inertiel \(\mathcal{R}’\), cette loi ne change absolument pas et respecte donc le principe de relativité. Pour le démontrer rigoureusement, il faut introduire la transformation de Galilée, que nous allons voir maintenant.
Transformation de Galilée
On se donne un certain référentiel inertiel \(\mathcal{R}\), et un autre référentiel \(\mathcal{R}’\) en mouvement rectiligne uniforme par rapport à \(\mathcal{R}\) avec une certaine vitesse \(\vec{u}\), et tels que les repères des deux référentiels coïncident à l’instant \(t=0\).
La transformation de Galilée est une formule qui permet de calculer les coordonnées \((t’, \vec{r}’)\) d’un objet dans le référentiel \(\mathcal{R}’\) en connaissant ses coordonnées \((t, \vec{r})\) dans \(\mathcal{R}\):
\[\begin{cases} t' &= t \\ \vec{r}' &= \vec{r} - t\vec{u} \end{cases}\]Pour simplifier les calculs, on peut se ramener au cas où \(\vec{u}=u \vec{e_x}\), et dans ce cas la transformation s’écrit:
\[\begin{cases} t' &= t \\ x' &= x - ut \\ y' &= y \\ z' &= z \end{cases}\]Avec cette formule, on peut facilement montrer que la deuxième loi de Newton est identique dans les deux référentiels, et respecte donc bien le principe de relativité:
\[\begin{align} \vec{r}' &= \vec{r} - \vec{u}t \\ \frac{d\vec{r}'}{dt'} &= \frac{d\vec{r}}{dt} - \frac{d(t\vec{u})}{dt} \\ \vec{v}' &= \vec{v} - \vec{u} \\ \vec{a}' &= \vec{a} \\ m\vec{a}' &= m\vec{a} = \vec{f} \end{align}\]Attention, cette démonstration fonctionne uniquement parce que le temps est absolu (et donc invariant par la transformation de Galilée), sinon on ne pourrait pas se permettre de calculer la dérivée par rapport au temps simultanément dans les deux référentiels.
Espace affine euclidien
Avant d’aller plus loin, il est utile de faire un petit détour mathématique en remarquant que dans la théorie de Galilée et Newton, on suppose que l’espace physique est un espace (mathématique) affine euclidien.
Pour le dire simplement, un espace affine est un ensemble de points sur lequel on peut former des vecteurs en reliant un point à un autre. C’est ce qu’on fait toujours depuis le collège, en écrivant par exemple \(\vec{r} = \vec{AB} = \vec{CD}\) ou encore \(\vec{AC} = \vec{AB} + \vec{BC}\) (relation de Chasles). L’idée cachée derrière ces expressions est qu’il y a un sens à parler d’égalité entre des vecteurs définis à des endroits différents de l’espace, ce qui n’a en fait rien d’évident, comme on le verra par la suite.
Pour préciser la définition, un espace affine euclidien est un espace affine dont les vecteurs sont munis d’un produit scalaire \(\langle\cdot,\cdot\rangle\), qui permet de définir des angles et longueurs. En particulier, une propriété bien connue des espaces euclidiens est le théorème de Pythagore:
\[\langle\vec{a},\vec{b}\rangle = 0 \iff \lVert\vec{a}+\vec{b}\rVert^2 = \lVert\vec{a}\rVert^2 + \lVert\vec{b}\rVert^2\]où \(\lVert\cdots\rVert\) est la norme euclidienne définie par \(\lVert\vec{v}\rVert^2 = \langle\vec{v},\vec{v}\rangle\).
Là encore, le fait que l’espace physique soit euclidien et donc vérifie le théorème de Pythagore n’a rien d’évident a priori, et la relativité générale montre justement qu’en fait ce n’est pas le cas !
Revenons un instant sur le produit scalaire car ce sera important pour la suite. Dans l’espace \(\mathbb{R}^3\) de la géométrie habituelle, un vecteur \(\vec{v}\) peut se représenter par ses coordonnées \((v^1, v^2, v^3)\). Attention, en relativité on écrit toujours les indices de coordonnées d’un vecteur en haut et non en bas, pour une raison que l’on verra plus loin. Dans ce cas on définit habituellement le produit scalaire par:
\[\langle\vec{a},\vec{b}\rangle = a^1 b^1 + a^2 b^2 + a^3 b^3\]Mais cette définition est juste un cas particulier; de façon générale, on définit un produit scalaire comme une “forme bilinéaire symétrique définie positive”, c’est-à-dire une application prenant deux vecteurs et retournant un nombre réel, vérifiant les propriétés suivantes:
- \(\langle\lambda\vec{a} + \vec{b},\vec{c}\rangle = \lambda\langle\vec{a},\vec{c}\rangle + \langle\vec{b},\vec{c}\rangle\) (linéaire à gauche)
- \(\langle\vec{a},\lambda\vec{b} + \vec{c}\rangle = \lambda\langle\vec{a},\vec{b}\rangle + \langle\vec{a},\vec{c}\rangle\) (linéaire à droite)
- \(\langle\vec{a},\vec{b}\rangle = \langle\vec{b},\vec{a}\rangle\) (symétrique)
- \(\vec{a} \neq \vec{0} \implies \langle\vec{a}, \vec{a}\rangle \gt 0\) (définie positive)
Le problème de la lumière
La mécanique de Galilée et Newton a connu de beaux succès pendant deux siècles, et a permis d’expliquer de nombreux phénomènes tels que le mouvement des planètes.
Mais au XIXe siècle, un gros problème est apparu à cause de la théorie de l’électromagnétisme. En effet, les équations de Maxwell qui permettent de calculer le champ électromagnétique (et en particulier la lumière) ne sont pas invariantes par la transformation de Galilée, et donc ne respectent pas le principe de relativité.
A cette époque, on pensait que la lumière se déplace dans un référentiel absolu appelé l’éther, mais si c’était le cas, alors la vitesse de la lumière mesurée par un observateur devrait dépendre du référentiel de cet observateur, plus exactement de sa vitesse par rapport à ce fameux éther. Mais voilà, la célèbre expérience de Michelson et Morley a montré en 1887 que la vitesse de la lumière mesurée sur Terre est toujours la même dans toutes les directions, ce qui contredisait l’existence de l’éther.
Suite à cette expérience, les physiciens Lorentz et Poincaré (qui croyaient toujours en l’existence de l’éther) ont tenté de réconcilier l’électromagnétisme avec le principe de relativité, en remplaçant la transformation de Galilée par une autre transformation appelée transformation de Lorentz, qui est compatible avec les équations de Maxwell tout en respectant le principe de relativité.
Mais c’est Einstein en 1905, avec sa théorie de la relativité restreinte, qui a trouvé une interprétation physique cohérente de la transformation de Lorentz (que Lorentz et Poincaré eux-mêmes n’arrivaient pas vraiment à expliquer), en postulant que l’éther n’existe pas et que les lois de la physique et la vitesse de la lumière sont invariantes dans tous les référentiels inertiels.
Transformation de Lorentz
Tout d’abord un petit point de vocabulaire: en relativité restreinte on appelle événement un point de l’espace à un certain instant. Dans un certain référentiel \(\mathcal{R}\), on peut donc repérer un événement par ses coordonnées \((t, x, y, z)\).
Comme on l’a vu précédemment, la physique de Galilée et Newton fait l’hypothèse que le temps est absolu, c’est-à-dire qu’on peut utiliser le même repère temporel quel que soit le référentiel. En particulier, il est possible de dire que deux événements ont lieu au même instant dans des référentiels différents.
Cette hypothèse nous semble assez intuitive, et pourtant il n’y a aucune raison physique pour que ce soit le cas. Une des clés de la relativité restreinte est donc de ne plus supposer que le temps est absolu, et voir ce que devient la formule de transformation des coordonnées d’un événement quand on passe d’un référentiel inertiel \(\mathcal{R}\) à un autre \(\mathcal{R}’\).
Pour mettre fin au suspense dès maintenant, voici donc cette formule, appelée transformation de Lorentz, dans le cas où \(\mathcal{R}’\) est en mouvement de translation rectiligne uniforme par rapport à \(\mathcal{R}\), à la vitesse \(\vec{u}=u \vec{e_x}\):
Si on pose \(\gamma = \frac{1}{\sqrt{1-u^2/c^2}}\), la transformation de Lorentz peut s’écrire:
\[\begin{cases} t' &= \gamma\left(t - \frac{ux}{c^2}\right) \\ x' &= \gamma(x - ut) \\ y' &= y \\ z' &= z \end{cases}\]\(c=3.10^8 m.s^{-1}\) étant la vitesse de la lumière.
Dans le cas où \(\vec{u}\) est de direction quelconque, la transformation est un peu plus compliquée et s’écrit:
\[\begin{cases} t' &= \gamma\left(t - \frac{\vec{u}.\vec{r}}{c^2}\right) \\ \vec{r}' &= \vec{r} + (\gamma-1)\left(\frac{\vec{u}.\vec{r}}{u^2}\right)\vec{u} - \gamma t\vec{u} \end{cases}\]Si on compare cette formule avec la transformation de Galilée, on voit que la principale différence est l’introduction du facteur \(\gamma\), appelé facteur de Lorentz, dont la valeur dépend de la vitesse du référentiel \(\mathcal{R}’\) par rapport à \(\mathcal{R}\).
On peut voir que si \(u\) est faible par rapport à la vitesse de la lumière, alors \(\gamma\) est proche de 1 et \(ux/c^2\) est proche de 0. Dans ce cas, on retombe (à peu près) sur la transformation de Galilée, qui est donc une approximation de la transformation de Lorentz pour les faibles vitesses.
Inversement, quand \(u\) se rapproche de \(c\), \(\gamma\) tend vers l’infini, ce qui est une façon de voir que \(u\) ne peut pas dépasser la vitesse de la lumière.
Nous reviendrons sur ce point par la suite, mais on voit déjà que dans la relativité restreinte, le temps dépend du référentiel choisi, ce qui est une révolution par rapport à la physique de Galilée et Newton !
Historiquement, Einstein avait pu démontrer la formule de transformation de Lorentz en faisant l’hypothèse que la vitesse de la lumière est identique dans tous les référentiels inertiels, mais il existe en fait une autre démonstration beaucoup plus élégante (mais assez laborieuse) se basant uniquement sur les hypothèses suivantes:
- l’espace est homogène (invariant par n’importe quelle translation) et isotrope (invariant par n’importe quelle rotation)
- le temps est uniforme (invariant par “translation”, c’est-à-dire changement d’origine)
C’est un résultat assez magique, car toute la théorie de la relativité restreinte, y compris l’invariance de la vitesse de la lumière, découle donc directement de ces deux hypothèses simples sur la structure de l’espace et du temps.
Espace-temps de Minkowski
Une conséquence de la transformation de Lorentz est que le temps et l’espace ne peuvent plus être considérés indépendamment comme c’était le cas avec le physique de Galilée et Newton. En effet, on voit qu’un changement de référentiel (inertiel) modifie à la fois les coordonnées spatiales et temporelle d’un événement, et qu’il n’y a plus de temps absolu. C’est pourquoi on ne parle plus de l’espace et du temps, mais tout simplement de l’“espace-temps”, qui est un espace à 4 dimensions: 1 dimension de temps et 3 dimensions d’espace. En pratique, on utilise souvent \(ct\) comme coordonnée temporelle au lieu de \(t\), car \(ct\) a la dimension d’une longueur et est donc homogène avec les coordonnées spatiales.
On peut alors se poser la question suivante: quelle est la structure mathématique de cet espace-temps ? Les mathématiciens Poincaré et Minkowski ont apporté une réponse à cette question en remarquant que si on se donne deux “points” de l’espace-temps (autrement dit deux événements) \(\mathbf{E_1}\) et \(\mathbf{E_2}\), il est possible de calculer une quantité appelée intervalle d’espace-temps qui est indépendante du référentiel choisi, autrement dit qui est invariante par la transformation de Lorentz.
Cet intervalle est noté \(\Delta s^2\) et vaut dans le référentiel \(\mathcal{R}\):
\[\begin{align} \Delta s^2 &= (c t_2-c t_1)^2 - (x_2-x_1)^2 - (y_2-y_1)^2 - (z_2-z_1)^2 \\ &= (c\Delta t)^2 - (\Delta l)^2 \end{align}\]Il suffit de faire le calcul pour voir que si on change de référentiel (inertiel) et qu’on calcule les coordonnées des deux événements dans le nouveau référentiel grâce à la transformation de Lorentz, la quantité \(\Delta s^2\) ne change pas et est donc bien définie de façon absolue.
On peut voir immédiatement que \(\Delta s^2\) ressemble beaucoup à la norme (au carré) d’un vecteur dans un espace affine euclidien dont les points auraient pour coordonnées \((ct, x, y, z)\), mais avec une différence de taille: il y a un signe \(-\) devant les termes \((x_2^i- x_1^i)^2\), alors que dans un vrai espace affine euclidien on aurait un signe \(+\) pour calculer la norme.
Pour avoir un espace affine, il faut pouvoir définir un vecteur entre deux points (ici deux événements). Si les coordonnées des événements \(\mathbf{E_1}\) et \(\mathbf{E_2}\) sont respectivement \((ct_1, x_1, y_1, z_1)\) et \((ct_2, x_2, y_2, z_2)\), alors on peut définir un vecteur \(\mathbf{u}=\vec{\mathbf{E_1} \mathbf{E_2}}\) à 4 dimensions appelé un quadrivecteur, reliant \(\mathbf{E_1}\) et \(\mathbf{E_2}\), et ayant pour coordonnées \((c t_2-c t_1, x_2-x_1, y_2-y_1, z_2-z_1)\) dans le référentiel \(\mathcal{R}\) (on notera en gras les quadrivecteurs).
En relativité, on numérote habituellement les coordonnées d’espace-temps de \(0\) à \(3\), \(0\) correspondant à la coordonnée temps et \(1\), \(2\) et \(3\) aux coordonnées d’espace. Les coordonnées du vecteur dans un certain référentiel s’écrivent donc \((u^0, u^1, u^2, u^3)\). Par convention, on désigne les indices des coordonnées d’espace-temps par des lettres grecques, donc on note aussi \(u^\alpha = (u^0, u^1, u^2, u^3)\). Attention, il ne faut pas confondre \(\mathbf{u}\) qui est le quadrivecteur lui-même, et \(u^\alpha\) qui est sa représentation dans un certain référentiel (le quadrivecteur est ce qu’il est, par contre ses coordonnées dépendent du référentiel choisi), même si par abus de notation on peut écrire \(\mathbf{u} = u^\alpha\).
Par analogie avec la vraie norme euclidienne, \(\Delta s^2\) est appelé la “pseudo-norme” (en fait la pseudo-norme au carré pour être exact) du vecteur d’espace-temps \(\mathbf{u}\). On voit facilement que cette pseudo-norme peut être obtenue à partir d’une sorte de produit scalaire (noté \(\eta\)), défini à partir des coordonnées des vecteurs de la façon suivante:
\[\eta(\mathbf{a}, \mathbf{b}) = a^0 b^0 - a^1 b^1 - a^2 b^2 - a^3 b^3\]A cause des signes \(-\), cette application \(\eta\) n’est pas un vrai produit scalaire car elle n’est pas définie positive (revoir la définition plus haut), même si les physiciens parlent parfois de produit scalaire par abus de langage. Plus formellement, l’application \(\eta\) est une “forme bilinéaire symétrique non dégénérée”, aussi appelée tenseur métrique, ou tout simplement une métrique (on devrait dire “pseudo-métrique” car elle n’est pas positive, mais c’est encore un abus de langage…).
Pour résumer, l’espace-temps est un espace affine de dimension 4, muni d’une (pseudo-)métrique dite de Minkowski. Cette métrique permet de définir une (pseudo-)distance entre deux événements, indépendante du référentiel choisi, et qu’on appelle un intervalle d’espace-temps.
Une conséquence absolument fondamentale et révolutionnaire de l’existence d’une métrique indépendante du référentiel est que l’espace-temps est absolu, alors que le temps et l’espace considérés séparément ne le sont pas (en effet la transformation de Lorentz montre que les distances et les durées dépendent du référentiel choisi).
Il y a donc un sens à parler d’un événement de l’espace-temps dans l’absolu, sans préciser le référentiel. Dans l’espace-temps de Minkowski, un référentiel est simplement un repère qui permet d’attribuer des coordonnées d’espace et de temps aux événements, et changer de référentiel revient simplement à choisir des coordonnées différentes.
Temps propre et dilatation du temps
Un phénomène bien connu expliqué par la relativité restreinte est celui de la “dilatation du temps”: on dit souvent que le temps “ralentit” ou qu’on vieillit “moins vite” quand on voyage rapidement. Ces affirmations sont à nuancer, car le temps en tant que tel n’a pas de vitesse donc ne peut pas vraiment ralentir, et si on dit “moins vite”, il faut toujours préciser par rapport à quoi.
Pour préciser ce qu’est la dilatation du temps, imaginons une fusée partant de la Terre (représentée par un point \(O\)) et voyageant à la vitesse \(u\) constante dans la direction de l’axe \((Ox)\). Dans ce scénario, on peut négliger les coordonnées \(y\) et \(z\), donc on se ramène à un espace-temps à 2 dimensions \(t\) et \(x\), ce qui ne change rien à l’explication. Nous avons donc un référentiel \(\mathcal{R}\) lié à la Terre, et un référentiel \(\mathcal{R}’\) lié à la fusée. Pour simplifier, on suppose que ces référentiels coïncident lors du décollage de la fusée, à l’instant \(t=t’=0\).
Supposons que Bernard voyage dans la fusée tandis que son frère jumeau Alain reste sur Terre, et que la fusée décolle le jour de leur 30ème anniversaire.
On considère les événements suivants \(\mathbf{E_1}\) et \(\mathbf{E_2}\):
- \(\mathbf{E_1}\): Bernard quitte la Terre, donc à l’instant \(t_1=t’_1=0\)
- \(\mathbf{E_2}\): Bernard fête son 31ème anniversaire, à l’instant \(t’_2=\tau=1\text{ an}\)
Comme on l’a vu, ces deux événements existent de façon absolue dans l’espace-temps, mais ont des coordonnées différentes dans \(\mathcal{R}\) et \(\mathcal{R}’\):
- \(\mathbf{E_1}\) a pour coordonnées \((0, 0)\) dans les deux référentiels (par construction)
- Dans \(\mathcal{R}’\), \(\mathbf{E_2}\) a pour coordonnées \((c\tau, 0)\), puisque \(x’_2=0\) (Bernard reste toujours immobile par rapport à la fusée)
- Dans \(\mathcal{R}\), \(\mathbf{E_2}\) a pour coordonnées \((ct_2, x_2) = (c\gamma\tau, u\gamma\tau)\), par application de la transformation de Lorentz
Si on calcule l’intervalle d’espace-temps entre \(\mathbf{E_1}\) et \(\mathbf{E_2}\), on trouve:
\[\begin{cases} \Delta s^2 &= c^2 \gamma^2\tau^2 - u^2\gamma^2\tau^2 = c^2\tau^2\gamma^2\left(1 - \frac{u^2}{c^2}\right) = (c\tau)^2 \text{ dans }\mathcal{R} \\ \Delta s^2 &= (c\tau)^2 \text{ dans }\mathcal{R}' \\ \end{cases}\]et donc comme prévu, l’intervalle est bien le même dans les deux référentiels.
Cet exemple montre que pour le même événement, il s’est écoulé 1 an pour Bernard depuis son départ, alors que dans le référentiel d’Alain il s’est écoulé \(\gamma\) ans, c’est-à-dire un temps plus long puisque \(\gamma\) est toujours \(\ge 1\) (par exemple si \(u=c/2\), alors \(\gamma\tau\) vaut environ 1 an et 2 mois).
Par définition, on appelle temps propre (noté \(\tau\)) de Bernard le temps mesuré dans “son” référentiel, c’est-à-dire un référentiel dans lequel il est immobile (ici \(\mathcal{R}’\)). De même la durée propre \(\Delta\tau\) est l’intervalle de temps propre entre deux événements. On voit ici que si on mesure le temps dans un autre référentiel que celui de Bernard (par exemple dans celui d’Alain), la durée entre deux événements le concernant est toujours plus grande que la durée propre. C’est en ce sens qu’on parle de “dilatation du temps” de Bernard vu depuis le référentiel d’Alain.
D’ailleurs la situation est totalement symétrique. Ainsi, si on considère maintenant l’événement \(\mathbf{E_3}\) “Alain fête son 31ème anniversaire” (donc à \(t_3=\tau\) et \(x_3=0\)), il s’est aussi écoulé un temps plus long (\(\gamma\tau\)) dans le référentiel de Bernard ! Cela peut sembler paradoxal, car si le temps de Bernard passe moins vite que celui d’Alain, comment le temps d’Alain peut-il aussi passer moins vite que celui de Bernard ? En fait il n’y a aucun paradoxe, mais pour s’en convaincre il est utile d’étudier la représentation graphique de l’espace-temps, appelée diagramme de Minkowski.
Diagramme de Minkowski et ligne d’univers
L’espace-temps étant de dimension 4, il est assez difficile de s’en faire une représentation intuitive, d’autant plus que ce n’est même pas un espace euclidien ! Une solution est de se limiter à une dimension d’espace (\(x\)) comme dans l’exemple précédent, et d’utiliser un diagramme de Minkowski qui est une représentation à 2 dimensions de l’espace-temps. Pour cela, il faut d’abord choisir un référentiel inertiel quelconque, et représenter en abscisses la coordonnée d’espace \(x\) dans ce référentiel, et en ordonnées la coordonnée de temps \(ct\). On représente aussi la droite d’équation \(x=ct\) qui matérialise la vitesse de la lumière.
Si on choisit \(\mathcal{R}\) comme référentiel, on peut alors représenter les événements de l’exemple précédent sur le diagramme grâce à leurs coordonnées \((ct,x)\):
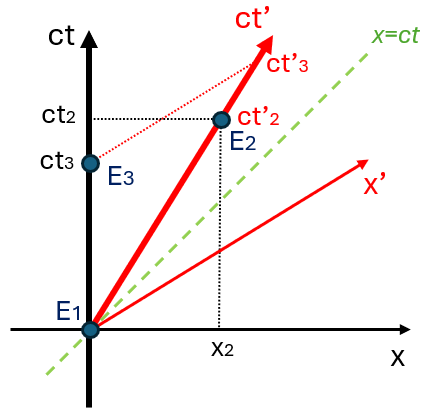
Ce diagramme contient beaucoup d’informations que l’on va détailler.
- La droite \((\mathbf{E_1} \mathbf{E_3})\) d’équation \(x=0\) (c’est-à-dire l’axe (\(ct\))) représente la trajectoire d’Alain dans l’espace-temps, et est appelée la ligne d’univers d’Alain.
- De même, la droite \((\mathbf{E_1} \mathbf{E_2})\) d’équation \(x=ut\) représente la trajectoire de Bernard, et est donc sa ligne d’univers. Cette droite représente aussi l’axe du temps (\(ct’\)) dans le référentiel \(\mathcal{R’}\), c’est-à-dire la droite d’équation \(x’=0\).
- On a aussi représenté l’axe de l’espace (\(x’\)) du référentiel \(\mathcal{R’}\), c’est-à-dire la droite d’équation \(t’=0\).
Le diagramme de Minkowski permet donc de représenter plusieurs référentiels sur le même schéma; on a ici en noir le référentiel \(\mathcal{R}\) et en rouge le référentiel \(\mathcal{R}’\), et on peut facilement voir quelles sont les coordonnées d’un événement dans un certain référentiel en projetant le point correspondant sur les axes de ce référentiel.
Mais il faut faire très attention, car encore une fois, l’espace de Minkowski n’est pas euclidien, et donc sa géométrie est un peu particulière ! En particulier, deux axes orthogonaux dans l’espace-temps (ce qui est le cas des axes de temps et d’espace dans un référentiel inertiel) ne sont pas perpendiculaires sur le diagramme de Minkowski, mais symétriques par rapport à la droite d’équation \(x=ct\) !
De même, il ne faut pas penser que l’intervalle d’espace-temps entre deux événements est représenté par la distance (euclidienne) entre les points correspondants sur le diagramme, car dans la métrique de Minkowski, la “longueur” de la composante spatiale d’un vecteur est comptée négativement. Par exemple, l’intervalle d’espace-temps entre \(\mathbf{E_1}\) et \(\mathbf{E_2}\) est exactement le même qu’entre \(\mathbf{E_1}\) et \(\mathbf{E_3}\) (et est égal à \(\Delta s^2 = (c\tau)^2\) comme on l’a vu précédemment), alors que ce n’est pas évident en regardant le diagramme.
Malgré ces quelques limitations, le diagramme de Minkowski permet de bien visualiser l’effet d’un changement de référentiel et le phénomène de “dilatation” du temps. On voit bien en effet que l’événement \(\mathbf{E_2}\) projeté dans le référentiel \(\mathcal{R}\) est “au-dessus” de l’événement \(\mathbf{E_3}\), ce qui traduit le fait que dans son référentiel propre, Alain fête son anniversaire “avant” celui de Bernard, alors que dans le référentiel \(\mathcal{R}’\) c’est exactement l’inverse: l’événement \(\mathbf{E_3}\) est “au-dessus” de \(\mathbf{E_2}\) et donc dans son référentiel Bernard fête aussi son anniversaire “avant” celui d’Alain ! Il n’y a donc pas de paradoxe, mais ce que montre le diagramme c’est qu’en relativité restreinte il n’y a aucun sens à parler d’“avant”, “après”, ou “en même temps” pour comparer \(\mathbf{E_2}\) et \(\mathbf{E_3}\).
Au passage, le diagramme de Minkowski montre aussi qu’un objet se déplaçant en ligne droite à vitesse constante dans un référentiel inertiel (c’est-à-dire soumis à aucune force) parcourt une ligne droite dans l’espace-temps, quel que soit le référentiel choisi. Ce n’est pas le cas d’un objet soumis à une accélération, qui dans ce cas parcourt une courbe dans l’espace-temps, même s’il se déplace en ligne droite dans l’espace. C’est un point fondamental sur lequel on reviendra en étudiant la relativité générale.
Cône de lumière
Une notion que nous n’avons pas encore abordée est celle de genre d’un intervalle d’espace-temps. On dit que l’intervalle \(\Delta s^2\) entre deux événements \(\mathbf{E_1}\) et \(\mathbf{E_2}\) est:
- de genre “temps” si \(\Delta s^2 \gt 0\)
- de genre “espace” si \(\Delta s^2 \lt 0\)
- de genre “lumière” si \(\Delta s^2 = 0\)
D’un point de vue physique, l’intervalle est de genre temps s’il existe un référentiel dans lequel \(\mathbf{E_1}\) et \(\mathbf{E_2}\) ont lieu au même endroit, et de genre espace s’il existe un référentiel dans lequel ils ont lieu au même instant. Enfin, l’intervalle est de genre lumière si on peut relier \(\mathbf{E_1}\) et \(\mathbf{E_2}\) par un rayon lumineux.
On peut visualiser les différents genres d’intervalles sur un diagramme de Minkowski:
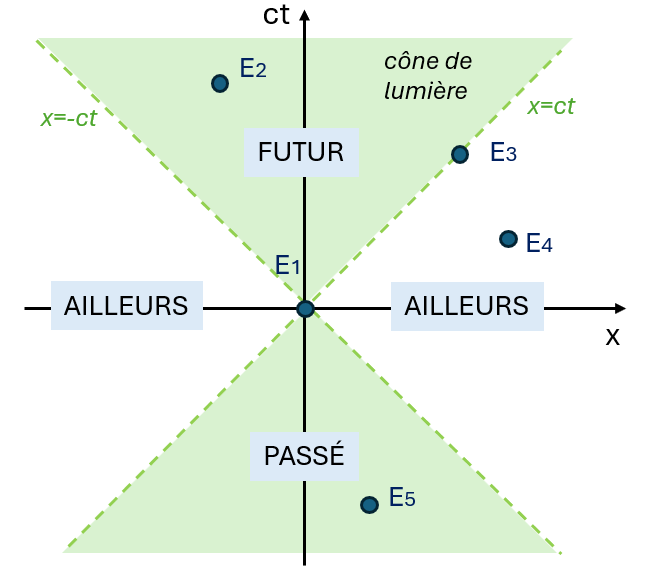
Ce diagramme représente ce qu’on appelle le cône de lumière centré sur l’événement \(\mathbf{E_1}\), qui est la zone délimitée par les trajectoires des rayons lumineux passant par \(\mathbf{E_1}\) (c’est-à-dire les droites d’équation \(x=\pm ct\)). L’intérieur du cône de lumière représente l’ensemble des événements pouvant être reliés à \(\mathbf{E_1}\) par un intervalle de genre temps, et est constitué de deux parties: le cône de lumière du futur (du côté \(ct\gt 0\)) et celui du passé (du côté \(ct\lt 0\)).
Ici, \(\mathbf{E_2}\) est donc situé dans le futur de \(\mathbf{E_1}\), et \(\mathbf{E_5}\) dans son passé. Dans ce cas, il y a bien un sens à dire que \(\mathbf{E_2}\) a lieu après \(\mathbf{E_1}\) et \(\mathbf{E_5}\) avant \(\mathbf{E_1}\), et ce dans n’importe quel référentiel.
L’extérieur du cône de lumière est appelé l’ailleurs, et représente l’ensemble des événements pouvant être reliés à \(\mathbf{E_1}\) par un intervalle de genre espace, par exemple \(\mathbf{E_4}\). Les événements ayant lieu dans l’ailleurs sont physiquement inaccessibles par \(\mathbf{E_1}\), car il faudrait dépasser la vitesse de la lumière pour les atteindre. Ces événements n’ont lieu ni avant, ni après \(\mathbf{E_1}\), mais juste… ailleurs.
Composition des vitesses
Supposons maintenant que Bernard lance un objet dans la fusée, à une vitesse \(\vec{v}’\) dans son référentiel \(\mathcal{R’}\). Quelle sera la vitesse de l’objet \(\vec{v}\) dans le référentiel d’Alain \(\mathcal{R}\) ?
Dans la relativité de Galilée, la loi de composition des vitesses est simplement \(\vec{v} = \vec{v}’ + \vec{u}\), mais en relativité restreinte, cette loi n’est plus valable car les coordonnées d’espace et de temps dépendent du référentiel.
Dans le cas où \(\vec{v}\) et \(\vec{u}\) sont colinéaires, la transformation de Lorentz montre que la loi de composition des vitesses devient:
\[v = \frac{v' + u}{1 + \frac{v'u}{c^2}}\]En particulier, cette loi montre que si \(v’=c\) alors on obtient toujours \(v=c\), et donc on retrouve bien que la vitesse de la lumière est invariante par changement de référentiel !
Quadrivitesse
A ce stade, on sait qu’un événement est défini de façon absolue dans l’espace-temps par un quadrivecteur dit temps-position, noté \(\mathbf{r}\). Dans un certain référentiel inertiel \(\mathcal{R}\), ce quadrivecteur peut se représenter par ses coordonnées \((ct, x, y, z)\), qu’on peut aussi écrire \((ct, \vec{r})\) en le décomposant en une partie temporelle et une partie spatiale.
De même, si on considère un objet en mouvement quelconque, on peut définir dans l’espace-temps son quadrivecteur vitesse, aussi appelé quadrivitesse, égal à:
\[\mathbf{v} = \frac{d\mathbf{r}}{d\tau}\]\(\tau\) étant le temps propre de l’objet, c’est-à-dire le temps mesuré dans un référentiel lié à l’objet lui-même.
Sur un diagramme de Minkowski, la quadrivitesse en un certain événement est un vecteur tangent à la ligne d’univers de l’objet au point en question (le temps propre \(\tau\) correspondant à l’abscisse curviligne de l’objet sur sa ligne d’univers, c’est-à-dire sa position sur la courbe):
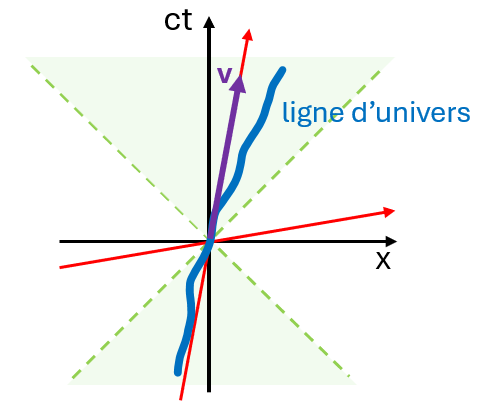
A partir de la transformation de Lorentz, on peut montrer que dans le référentiel \(\mathcal{R}\), les coordonnées de la quadrivitesse sont:
\[v^\alpha = \left(\gamma c, \gamma\frac{dx}{dt},\gamma\frac{dy}{dt},\gamma\frac{dz}{dt}\right) = (\gamma c,\gamma \vec{v})\]avec \(\vec{v}=\frac{d\vec{r}}{dt}\) et \(\gamma(v)=\frac{1}{\sqrt{1-v^2/c^2}}\).
On remarque que même si les coordonnées de la quadrivitesse dépendent du référentiel, sa norme (de Minkowski) est invariante par changement de référentiel et vaut toujours \(\eta(\mathbf{v}, \mathbf{v}) = c^2\). D’une certaine façon, on peut donc dire qu’objet se déplace toujours “à la vitesse de la lumière” dans l’espace-temps.
Bien que la vitesse dans l’espace soit relative au référentiel, la quadrivitesse est donc, elle, bien définie de façon absolue dans l’espace-temps de Minkowski.
Dynamique relativiste
Maintenant, voyons ce que devient la loi fondamentale de la dymamique de Newton. En physique classique, si on considère un corps de masse \(m\) soumis à une force \(\vec{f}\), alors on peut écrire cette loi sous la forme:
\[\frac{d\vec{p}}{dt} = \vec{f}\]où \(\vec{p}=m\vec{v}\) est la quantité de mouvement du corps en question.
Mais en relativité restreinte, la transformation de Lorentz montre que cette équation n’est pas invariante par changement de référentiel, et donc que cette loi ne respecte plus le principe de relativité (alors que c’était le cas en relativité galiléenne).
A partir de la loi de composition des vitesses, on peut montrer que la loi fondamentale de la dynamique fonctionne bien si on prend comme nouvelle définition de la quantité de mouvement:
\[\vec{p} = \gamma m \vec{v}\]où \(m\) est la masse du corps au repos et \(\gamma(v)\) le facteur de Lorentz habituel.
Avec cette définition, \(\vec{p}\) dépend bien sûr du référentiel choisi. Mais de la même façon que pour la position et la vitesse, on peut se demander s’il existe un existe un équivalent de la quantité de mouvement dans l’espace-temps, qui serait invariant par changement de référentiel.
Et effectivement, par analogie avec la quadrivitesse, on peut dire que dans un certain référentiel, \(\vec{p}\) est la partie spatiale d’un quadrivecteur \(\mathbf{p}\) appelé quadri-impulsion, ayant pour composantes:
\[p^\alpha = (\gamma m c, \gamma m \vec{v})\]et donc plus généralement, la quadri-impulsion s’écrit indépendamment du référentiel:
\[\mathbf{p} = m\mathbf{v}\]La partie spatiale de la quadri-impulsion (\(\gamma m \vec{v}\)) correspond à la quantité de mouvement habituelle, mais quelle est donc la signification physique de sa partie temporelle \(\gamma m c\) ? Il y a plusieurs façon de le voir, mais on peut par exemple remarquer que si \(v\) est faible, on a:
\[\gamma m c^2 \approx mc^2+\frac{1}{2}mv^2\]On reconnait dans la partie de droite \(\frac{1}{2}mv^2\) l’énergie cinétique du corps, due à sa vitesse, et on voit apparaître un terme constant \(mc^2\) qu’on appelle énergie de masse. On peut donc poser \(E=\gamma m c^2\), \(E\) représentant l’énergie (totale) du corps, ce qui donne:
\[p^\alpha = \left(\frac{E}{c}, \gamma m \vec{v}\right) = \left(\frac{E}{c}, \vec{p}\right)\]C’est pourquoi \(\mathbf{p}\) est aussi appelé le quadrivecteur énergie-impulsion, car sa partie temporelle représente l’énergie du corps, et sa partie spatiale représente son impulsion (l’autre nom de la quantité de mouvement).
Si on calcule la pseudo-norme de \(\mathbf{p}\) dans un référentiel quelconque et dans le référentiel propre du corps, on trouve bien une valeur indépendante du référentiel:
\[\eta(\mathbf{p},\mathbf{p}) = \frac{E^2}{c^2}-p^2 = m^2c^2\]avec \(p=\gamma m v = \frac{mv}{\sqrt{1-v^2/c^2}}\).
On obtient donc une formule fondamentale appelée relation d’Einstein: \(E^2 = m^2 c^4 + p^2 c^2\).
Si on se place dans le référentiel propre du corps, alors \(p=0\) et on trouve donc… \(E=mc^2\) !
On peut maintenant généraliser la loi fondamentale de la dynamique dans l’espace-temps, en définissant la quadri-force par:
\[\mathbf{f} = \frac{d\mathbf{p}}{d\tau}\]Si on se place dans un certain référentiel, les coordonnées de la quadri-force sont donc:
\[f^\alpha = \left(\frac{1}{c}\frac{dE}{d\tau}, \frac{d\vec{p}}{d\tau}\right) = \left(\frac{\gamma}{c}\frac{dE}{dt}, \gamma\frac{d\vec{p}}{dt}\right)\]Avec un peu de calcul, on peut montrer que \(\frac{dE}{dt} = \vec{f}.\vec{v}\) (c’est la version relativiste du théorème de l’énergie cinétique), et donc:
\[f^\alpha = \left(\gamma\vec{f}.\frac{\vec{v}}{c}, \gamma\vec{f}\right)\]A SUIVRE dans la 2ème partie: principe d’équivalence, variétés différentielles, fibré tangent, dérivée covariante…