Introduction à la Relativité (2ème partie)
- De la relativité restreinte à la relativité générale
- Principe d’équivalence
- L’ascenseur d’Einstein
- Courbure de l’espace-temps
- Variétés différentielles
- Vecteurs tangents
- Espace vectoriel tangent
- Fibré tangent et champ de vecteurs
- Connexion affine
- Transport parallèle et géodésiques
De la relativité restreinte à la relativité générale
Dans la 1ère partie consacrée à la relativité restreinte, nous avons vu que les travaux de Lorentz, Poincaré, Einstein et Minkowsi ont abouti à la découverte de l’espace-temps et de sa structure géométrique.
Pour rappel, l’espace-temps permet de réécrire les lois de la physique de manière élégante, en utilisant des quadrivecteurs (position, vitesse, force, etc.) indépendants du référentiel inertiel choisi. En particulier, le principe d’inertie nous dit qu’un corps soumis à aucune force doit se déplacer en ligne droite dans l’espace-temps, c’est-à-dire avec une quadrivitesse \(\mathbf{v}\) constante.
La théorie de la relativité restreinte a cependant un maillon faible: la gravitation. Dans la théorie de la gravitation de Newton, deux corps de masse \(m_1\) et \(m_2\) séparés par une distance \(r\) s’attirent mutuellement avec une force \(F=G\frac{m_1 m_2}{r^2}\). Mais cette loi n’est pas compatible avec la relativité restreinte, car elle n’est pas invariante par la transformation de Lorentz, et de plus elle suppose qu’un corps puisse en influencer un autre à distance et instantanément, ce qui est normalement impossible car aucune information ne peut voyager plus vite que la lumière.
C’est donc en cherchant une loi de la gravitation compatible avec la relativité restreinte qu’Einstein a mis au point sa théorie de la relativité générale, achevée en 1915.
Principe d’équivalence
Toute la réflexion d’Einstein s’est construite à partir du principe d’équivalence, qui était déjà connu depuis Galilée:
Tous les corps soumis à un même champ de gravitation chutent à la même vitesse (dans le vide)
Ce qu’on appelle champ de gravitation est un vecteur \(\vec{\mathcal{G}}\) défini en chaque point de l’espace (c’est-à-dire un champ de vecteurs), tel que la force de gravitation s’exerçant sur un corps de masse \(m\) soit égale à \(\vec{f} = m\vec{\mathcal{G}}\).
En appliquant la deuxième loi de Newton, on peut donc calculer l’accélération d’un corps dans un champ de gravitation:
\[\begin{align} m\vec{a} &= \vec{f} \\ m\vec{a} &= m\vec{\mathcal{G}} \\ \vec{a} &= \vec{\mathcal{G}} \\ \end{align}\]On voit donc que l’accélération d’un corps (et donc sa vitesse) dépend uniquement du champ de gravitation, et pas de sa masse. Mais cette démonstration fonctionne uniquement grâce à une hypothèse très forte: la masse qui apparaît dans l’expression \(m\vec{a}\), appelée masse inerte, doit être égale à la masse qui apparaît dans l’expression \(m\vec{\mathcal{G}}\), appelée masse pesante.
Cette égalité entre masse inerte (qui s’oppose au mouvement) et masse pesante (qui réagit au champ de gravitation) est une autre façon d’exprimer le principe d’équivalence, et elle a été vérifiée expérimentalement de façon extrêmement précise.
C’est en réfléchissant au principe d’équivalence qu’Einstein a eu l’intuition que la gravitation n’est pas une force comme les autres, et que l’égalité entre masse inerte et masse pesante n’est sans doute pas un hasard.
L’ascenseur d’Einstein
Pour appuyer sa réflexion, Einstein a imaginé l’expérience de pensée suivante. Supposons qu’un observateur soit enfermé dans un ascenseur lâché en chute libre au dessus du sol. L’observateur va chuter à la même vitesse que l’ascenseur, et donc flotter comme s’il n’était pas soumis au champ de pesanteur terrestre. Pour cet observateur, la situation est exactement la même que si l’ascenseur était immobile dans l’espace, en dehors de tout champ de gravitation (en imaginant que ce soit possible). Inversement, si l’ascenseur est placé dans l’espace et accéléré vers le haut (avec une accélération égale à \(g=9.81 m s^{-2}\)), l’observateur ne pourra pas faire la différence avec un ascenseur immobile posé à la surface de la Terre et soumis au champ de gravitation terrestre.
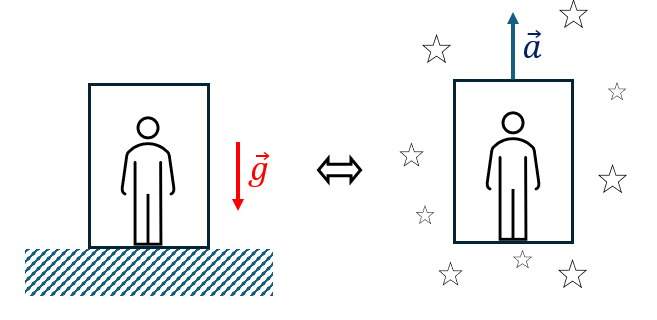
D’après Einstein, le principe d’équivalence peut donc s’énoncer de cette façon:
Aucune expérience de physique ne peut permettre de distinguer un référentiel accéléré d’un référentiel non accéléré mais soumis à un champ de gravitation
De la même façon, si on se place dans un référentiel en chute libre dans un champ de gravitation, l’effet de ce champ de gravitation est (localement) annulé, car tout se passe comme s’il n’y avait pas de force de gravitation du tout. Un référentiel en chute libre se comporte donc exactement comme un référentiel inertiel, dans lequel un corps soumis à aucune force (en ignorant la gravitation) reste immobile ou en mouvement rectiligne uniforme.
Einstein a poursuivi le raisonnement en postulant que la gravitation n’est pas une force, et que les vrais référentiels inertiels ne sont en fait pas les référentiels galiléens (c’est-à-dire en mouvement rectiligne uniforme), mais les référentiels en chute libre ! Avec ce raisonnement, la force de gravitation n’est rien d’autre qu’une force fictive, tout comme les forces d’inerties qui apparaissent en mécanique classique quand on se place dans un référentiel accéléré (un exemple bien connu étant la “force” centrifuge ressentie dans un manège en rotation).
Courbure de l’espace-temps
Comme on l’a vu, d’après la relativité restreinte, un corps soumis à aucune force doit se déplacer en ligne droite dans l’espace-temps, indépendamment du référentiel choisi. Or, si on représente la ligne d’univers d’un corps accéléré (par exemple notre ascenseur en chute libre) sur un diagramme de Minkowski, on voit que ce corps décrit une trajectoire courbe, et non une droite:
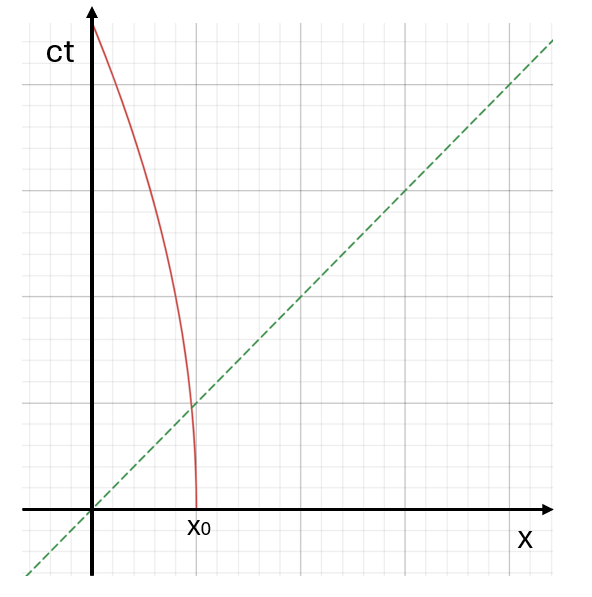
L’intuition d’Einstein pose donc problème: comment un corps en chute libre peut-il avoir une trajectoire courbe (puisqu’il est accéléré), mais en ligne droite (puisqu’il n’est soumis à aucune vraie force) ?
C’est là qu’arrive la dernière pièce du puzzle: la solution est que c’est l’espace-temps lui-même qui est courbe ! En effet dans un espace courbe, par exemple sur la surface d’une sphère, la géométrie euclidienne (c’est-à-dire la géométrie habituelle qu’on apprend à l’école) ne s’applique plus, et les lignes droites ne sont plus définies de la même façon que dans un espace plat (sans courbure). Par exemple si on représente sur une carte du monde le trajet d’un avion qui effectue un vol direct Paris New-York, donc en “ligne droite”, on voit que cette ligne droite (on parle en fait de géodésique) est en fait une courbe, ce qui donne une bonne intuition de ce qu’est une géométrie courbe:
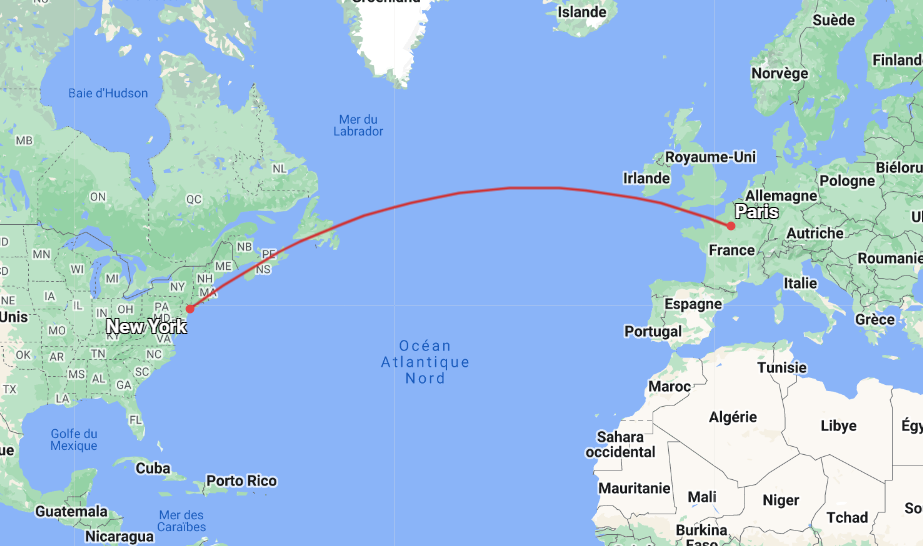
Il est déjà difficile de se faire une représentation intuitive de l’espace-temps de Minkowski, qui est un espace plat à 4 dimensions, alors on peut sans peine comprendre que décrire un espace courbe à 4 dimensions ne va pas être simple ! Albert Einstein lui-même a eu besoin de l’aide de son ami mathématicien Marcel Grossmann pour mettre en place tout le formalisme mathématique nécessaire à sa théorie de la relativité générale, ce qui lui a pris plusieurs années.
Toute la théorie de la relativité générale consiste donc à décrire ce que signifie précisément la “courbure de l’espace-temps”, et à exprimer la loi de la gravitation en termes de courbure, c’est-à-dire à déterminer comment la masse des corps (étoiles, planètes, etc.) modifie cette courbure de l’espace-temps.
En relativité générale, toutes les notions habituelles de la géométrie euclidienne et de la physique (vecteurs, distances, vitesse, etc.) doivent être oubliées et complètement redéfinies en partant de zéro. Dans les chapitres suivants, nous allons donc voir progressivement comment décrire mathématiquement un espace-temps courbe, pour finalement arriver à l’équation d’Einstein qui décrit la géométrie de l’espace-temps: \(G^{\mu\nu} = \kappa T^{\mu\nu}\).
Variétés différentielles
En relativité restreinte, nous avons vu que si on choisit un certain référentiel, on peut repérer les événements de l’espace-temps de Minkowski par leurs coordonnées dans l’espace \(\mathbb{R}^4\). Il est important de remarquer que ces coordonnées sont globales sur l’ensemble de l’espace-temps, et que par construction l’espace-temps a les mêmes propriétés partout, en particulier la notion de (pseudo-)distance entre deux événements. Rappelons également que cet espace-temps est un espace affine, c’est-à-dire qu’on peut toujours définir un vecteur reliant un événement à un autre.
En relativité générale, l’espace-temps est modélisé par un objet mathématique appelé une variété différentielle (lisse), de dimension 4. De façon générale, on appelle variété (manifold en anglais) de dimension \(n\) un espace (topologique) \(M\) qui “ressemble” à \(\mathbb{R}^n\) au voisinage de chaque point (mathématiquement on dit que \(M\) est localement homéomorphe à \(\mathbb{R}^n\)).
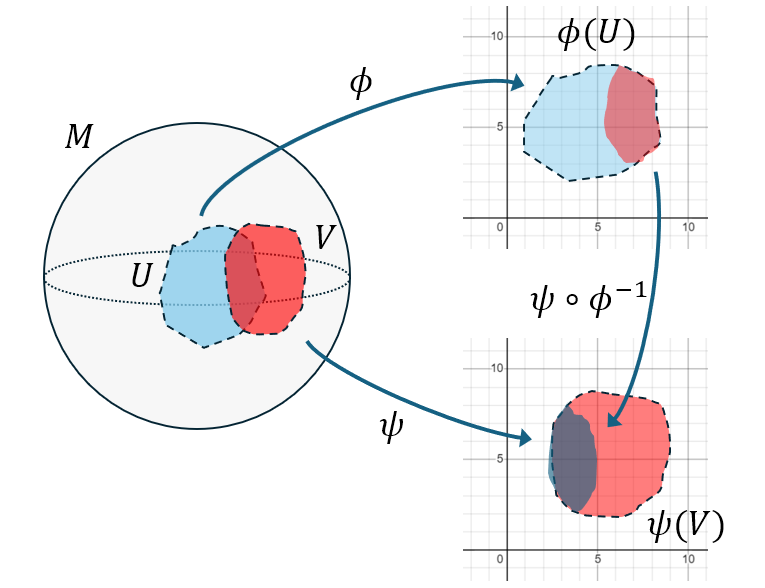
Plus précisément, autour de chaque point de la variété, il existe un voisinage (ouvert) \(\mathcal{U}\) de ce point, sur lequel on peut définir un système de coordonnées dans \(\mathbb{R}^n\), aussi appelé une carte. Formellement, une carte est un couple \((\mathcal{U}, \phi)\), où \(\phi\) est une application de \(\mathcal{U} \subset M\) dans \(\phi(\mathcal{U}) \subset \mathbb{R}^n\), ayant de “bonnes” propriétés (elle doit être bijective, continue, et de réciproque continue). Si \(p\) est un point de \(\mathcal{U}\), alors \(\phi(p) = (x^0, x^1, …, x^{n-1})\) représente les coordonnées de \(p\) dans la carte \((\mathcal{U}, \phi)\). Réciproquement, si \(x^\alpha = (x^0, x^1, …, x^{n-1})\), alors \(p=\phi^{-1}(x^\alpha)\) est le point de coordonnées \(x^\alpha\).
Pour illustrer ce concept, voici un exemple de carte sur une sphère, qui est une variété de dimension 2:
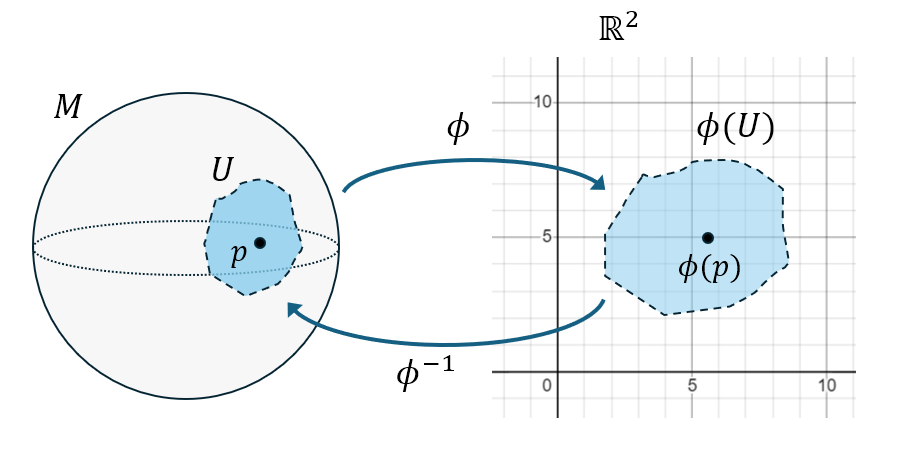
Dans le cas général, il n’est pas possible de représenter entièrement la variété sur \(\mathbb{R}^n\) avec une seule carte. C’est un problème bien connu lorsqu’on essaie de dessiner une carte de la Terre sur un plan: quelque soit la méthode de projection choisie, il y a toujours un point (par exemple le pôle nord) auquel on ne peut pas attribuer de coordonnées de façon unique sur la carte. Pour représenter entièrement une sphère sur \(\mathbb{R}^2\), il faut donc au moins deux cartes.
On appelle (assez logiquement) un atlas un ensemble de cartes qui recouvrent entièrement une variété.
Quand deux cartes \((\mathcal{U}, \phi)\) et \((\mathcal{V}, \psi)\) d’un atlas ont une intersection non vide, on veut pouvoir “facilement” passer d’une carte à l’autre (c’est-à-dire changer de système de coordonnées), plus précisément on veut que l’application \(\psi\circ\phi^{-1}\) soit de classe \(C^\infty\) (c’est-à-dire indéfiniment différentiable). On dit dans ce cas que l’atlas est lisse.
Enfin, on appelle variété différentielle lisse une variété munie d’un atlas lisse, ce qui est le cas de l’espace-temps en relativité générale. Dans la suite on parlera simplement de “variété”, sans préciser à chaque fois qu’elle est lisse.
Attention, le choix d’un atlas est complètement arbitraire et ne donne aucune information sur la variété elle-même. En particulier, la distance entre deux points sur une carte ne permet pas (à ce stade en tout cas) de donner une mesure de distance entre les deux points correspondants sur la variété. De même, le fait que trois points soient alignés sur une certaine carte ne dit pas du tout que ces points sont “alignés” sur la variété. Le choix d’un atlas permet simplement d’attribuer des coordonnées numériques aux points de la variété, ce qui permettra par la suite de faire des calculs sur ces points.
Vecteurs tangents
Pour décrire des lois de la physique, nous avons au minimum besoin d’une notion de vecteur, par exemple pour représenter la vitesse d’un corps. Mais dans une variété, il n’y a en général aucun sens à parler d’un vecteur entre deux points (par exemple, quel pourrait bien être le vecteur “pôle nord - pôle sud” sur une sphère ?), et il faut donc trouver autre chose.
L’idée est qu’il est tout de même possible de définir des vecteurs en un point \(p\) de la variété, grâce aux notions de vecteur tangent et de dérivée directionnelle, que nous allons voir maintenant.
Tout d’abord il faut donner quelques définitions:
- Une fonction à valeurs réelles sur la variété \(M\) (aussi appelée champ scalaire) est une application \(f\) de \(M\) dans \(\mathbb{R}\). Une fonction est lisse si sa représentation \(f \circ \phi^{-1}\) dans n’importe quelle carte est lisse (c’est-à-dire de classe \(C^\infty\)). On note \(C^\infty(M)\) l’ensemble des fonctions lisses sur la variété \(M\).
- Une courbe lisse sur la variété \(M\) est une application \(\gamma\) de \(\mathbb{R}\) dans \(M\), qui à un paramètre \(\lambda\) réel associe un point \(\gamma(\lambda)\) de la variété, telle que sa représentation \(\phi\circ\gamma\) dans n’importe quelle carte soit lisse.
Prenons maintenant une courbe lisse \(\gamma\) passant par le point \(p\) (on prendra \(\gamma(0)=p\) pour simplifier), et une carte \((\mathcal{U}, \phi)\) au voisinage de \(p\).
On notera \({x^\alpha}\) l’application \(\phi\circ\gamma\) (de \(\mathbb{R}\) dans \(\mathbb{R}^n\)), qui représente les coordonnées de la courbe \(\gamma\) dans la carte, et \(\dot{x}^\alpha\) la dérivée de \(x^\alpha\) par rapport à \(\lambda\). Dans \(\mathbb{R}^n\), le vecteur tangent \(\mathbf{v}\) à la courbe \(x^\alpha(\lambda)\) au point \(x^\alpha(0)=\phi(p)\) a alors pour coordonnées:
\[v^\alpha = \dot{x}^\alpha(0)=(\phi\circ\gamma)'(0)\]Si le paramètre \(\lambda\) est le temps, et \(x^\alpha(\lambda)\) la trajectoire d’un point mobile, \(\mathbf{v}\) est tout simplement le vecteur vitesse de ce point mobile en \(\lambda=0\), obtenu en calculant la dérivée de la position par rapport au temps.
On considère maintenant une fonction lisse \(f\) quelconque sur la variété. La fonction \(f\circ\gamma\) est donc une fonction de \(\mathbb{R}\) dans \(\mathbb{R}\). On appelle dérivée directionnelle de \(f\) dans la direction de la courbe \(\gamma\) au point \(p\) le nombre:
\[D_{\mathbf{\gamma}}f(p) = (f\circ\gamma)'(0)\]Le schéma suivant représente la courbe \(\gamma\), le vecteur tangent \(\mathbf{v}\) et la fonction \(f\) (matérialisée par ses lignes de niveau en vert, comme sur une carte topographique), sur la variété et sur la carte \(\phi\). Si on imagine que \(f\) représente l’altitude d’un point sur la Terre, la dérivée directionnelle \(D_{\mathbf{\gamma}}f(p)\) s’interprète comme étant la pente du chemin quand on avance dans la direction de la courbe, c’est-à-dire dans la direction du vecteur tangent \(\mathbf{v}\).
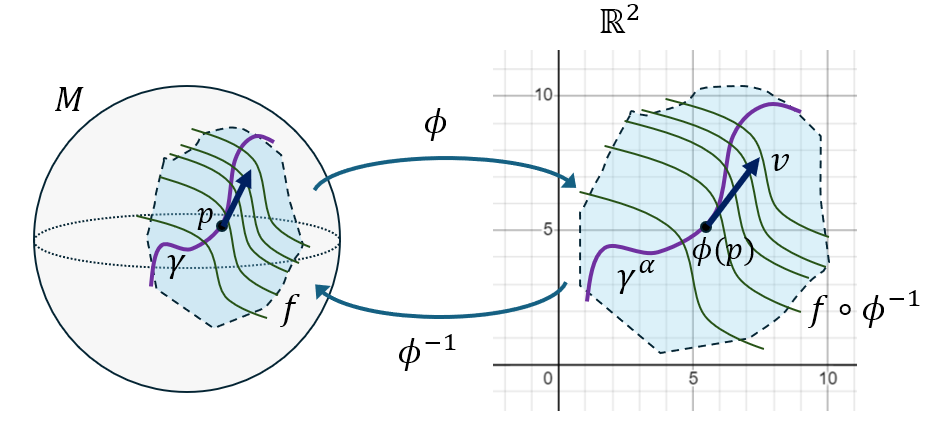
On peut montrer que dans la carte \(\phi\), la dérivée directionnelle peut s’écrire:
\[\begin{align} D_{\mathbf{\gamma}}f(p) &= \sum_{\alpha=0}^{n-1} v^\alpha \left.\partial_\alpha(f\circ \phi^{-1})\right\rvert_{\phi(p)}\\ &=\sum_{\alpha=0}^{n-1} v^\alpha \left.\frac{\partial f}{\partial x^\alpha}\right\rvert_{p}\\ \end{align}\]en ayant introduit la notation suivante:
\[\frac{\partial f}{\partial x^\alpha} := \partial_\alpha (f\circ \phi^{-1})\]qui permet d’exprimer la \(\alpha^\text{ème}\) dérivée partielle de la fonction \(f\) représentée dans la carte \(\phi\). Il faut bien voir que c’est un abus de notation, car \(f\) n’est pas une fonction définie sur \(\mathbb{R}^n\), mais sur \(M\). Il faut faire attention en utilisant cette notation car elle suppose que les coordonnées \(x^\alpha\) sont exprimées dans une certaine carte \(\phi\), qui n’est pas précisée.
A partir du vecteur \(\mathbf{v}\), on peut donc calculer la dérivée directionnelle de n’importe quelle fonction lisse \(f\), et réciproquement on peut montrer que si on connait la fonction “dérivée directionnelle” qui à une fonction lisse \(f\) quelconque associe le nombre \(D_{\mathbf{\gamma}}f(p)\), alors on peut retrouver le vecteur \(\mathbf{v}\).
L’astuce consiste donc à définir le vecteur tangent à la courbe \(\gamma\) sur la variété \(M\) au point \(p\) (noté \(V_{\gamma,p}\)) comme étant l’opérateur “dérivée directionnelle” dans la direction de la courbe:
\[\begin{align} V_{\gamma,p}: C^\infty(M) &\longrightarrow \mathbb{R}\\ f &\longmapsto V_{\gamma,p}(f) = (f\circ\gamma)'(0) \end{align}\]Grâce à cette définition, on a donc bien introduit une notion de vecteur en un point de la variété, et ce indépendamment de la carte choisie. Dans ce contexte, un vecteur est donc une application (qu’on appelle dans ce cas une fonctionnelle) qui à une fonction associe un nombre.
Cette définition peut sembler bien abstraite et compliquée, mais elle a l’avantage d’être intrinsèque, c’est-à-dire qu’elle ne suppose pas que la variété soit “plongée” dans un espace de plus grande dimension, comme par exemple la sphère représentée dans un espace à 3 dimensions sur les schémas précédents. En effet, il est important de comprendre qu’en relativité générale, l’espace-temps (qui une variété de dimension 4) existe en tant que tel et n’est pas plongé dans un espace plus grand.
Espace vectoriel tangent
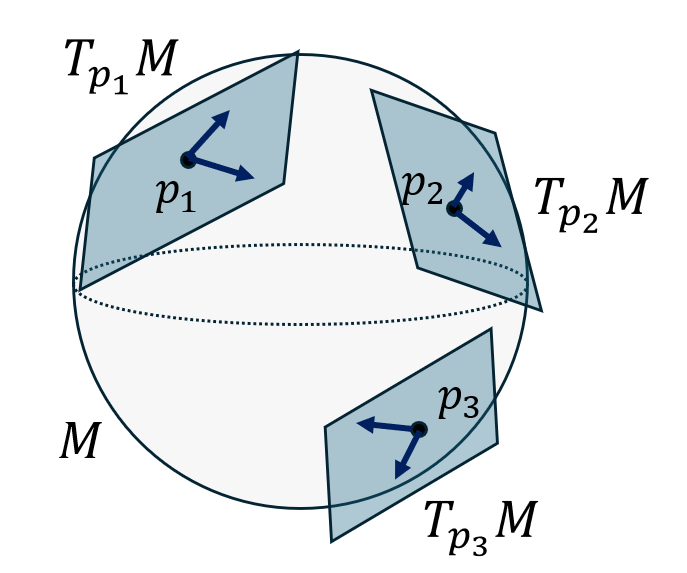
Puisqu’il existe une infinité de courbes passant par un point \(p\), on peut définir un ensemble de tous les vecteurs tangents en ce point. Cet ensemble est appelé l’espace tangent à la variété \(M\) au point \(p\), et est noté \(T_p M\).
On peut montrer que \(T_p M\) est un espace vectoriel sur \(\mathbb{R}\) (de dimension \(n\)), c’est-à-dire qu’on peut additionner des vecteurs tangents en un point, ou les multiplier par un nombre réel, avec les propriétés habituelles des opérations sur les vecteurs. Attention, on ne peut pas additionner des vecteurs définis en des points différents de la variété, mais uniquement au même point !
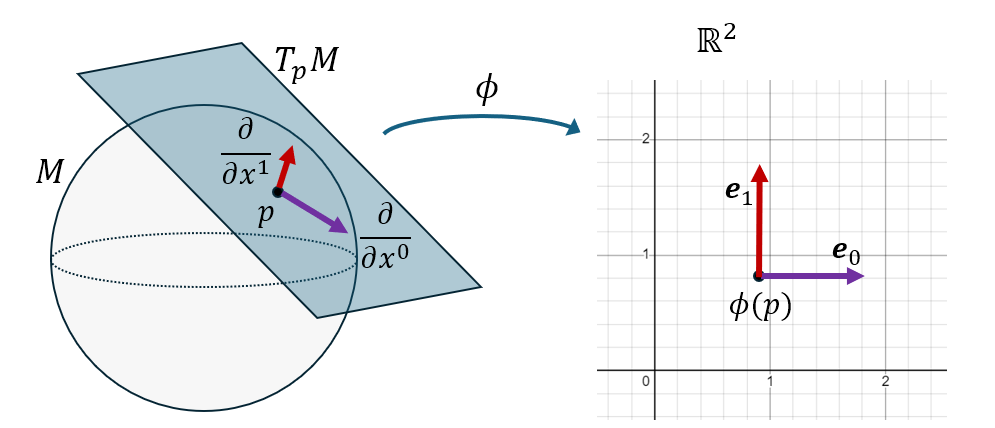
Si on se place dans une certaine carte \(\phi\), on peut montrer que tous les vecteurs de \(T_p M\) sont de la forme:
\[V =\sum_{\alpha=0}^{n-1} V^\alpha \left.\frac{\partial}{\partial x^\alpha}\right\rvert_{p}\]Autrement dit, un vecteur tangent peut toujours s’écrire comme une combinaison linéaire des opérateurs “dérivée partielle” dans la carte \(\phi\). Ces opérateurs forment une base de l’espace vectoriel \(T_p M\), et correspondent en fait aux dérivées directionnelles selon les \(n\) vecteurs de base \((\mathbf{e}_\alpha)\) de \(\mathbb{R}^n\).
Au passage, il est temps d’introduire la convention de sommation d’Einstein, qui consiste à sous-entendre le signe “somme” sur un indice muet (ici \(\alpha\)) quand cet indice apparaît deux fois (une fois “en haut” et une fois “en bas”, nous reverrons ce point plus loin) dans une expression. Avec cette convention, on peut donc simplement écrire un vecteur tangent sous la forme:
\[V = V^\alpha \left.\frac{\partial}{\partial x^\alpha}\right\rvert_{p}\]Voici une représentation géométrique d’un espace tangent, avec ses vecteurs de base:
Fibré tangent et champ de vecteurs
L’ensemble de tous les vecteurs (tangents) d’une variété \(M\) est appelé son fibré tangent, noté \(TM\). Plus exactement, le fibré tangent est l’ensemble des couples \((p, V)\), avec \(p \in M\) et \(V \in T_p M\).
En effet il faut rappeler que dans une variété, un vecteur tangent est toujours défini en un point donné, c’est pourquoi on considère toujours des couples \((p, V)\) et pas simplement des vecteurs \(V\) pris isolément, comme on pouvait le faire dans un espace affine tel que l’espace de Minkowski.
On peut montrer que le fibré tangent est lui-même une variété lisse, de dimension \(2n\). Il faut \(n\) coordonnées pour représenter le point \(p\) dans une carte, et encore \(n\) coordonnées pour représenter le vecteur \(V\). Plus précisément, dans une certaine carte \(\phi\), les coordonnées d’un élément \((p, V)\) de \(TM\) peuvent s’écrire sous la forme:
\[\left(x^0, x^1, ..., x^{n-1}, V^0, V^1, ..., V^{n-1}\right)\]où \(V^\alpha\) sont les coordonnées de \(V\) dans la base vue précédemment:
\[\left(\left.\frac{\partial}{\partial x^0}\right\rvert_{p}, \left.\frac{\partial}{\partial x^1}\right\rvert_{p}, ..., \left.\frac{\partial}{\partial x^{n-1}}\right\rvert_{p}\right)\]On définit ensuite un champ de vecteurs \(X\) sur la variété comme une application (lisse) de \(M\) dans \(TM\), qui à chaque point \(p \in M\) associe un vecteur tangent \(X(p) \in T_p M\) (\(X\) est aussi appelé une section du fibré tangent \(TM\)).
L’ensemble de tous les champs de vecteurs sur la variété est noté \(\Gamma(TM)\).
Connexion affine
Comme on l’a dit, il n’y a a priori aucun lien entre deux vecteurs définis en des points différents de la variété. Il n’y a donc par exemple aucun sens à dire qu’un champ de vecteurs est uniforme (c’est-à-dire égal en tout point), comme on pouvait le faire dans un espace affine.
Cependant, si on reste au voisinage d’un point \(p\) de la variété, il est possible de définir localement une notion de dérivée d’un champ de vecteur, qui permet de quantifier la variation du champ de vecteur d’un point à un autre. Cette dérivée est appelée une connexion affine, ou encore une dérivée covariante.
Pour comprendre ce qu’est une connexion, il faut d’abord revenir sur la notion de dérivée directionnelle vue précédemment. Si on se donne une fonction \(f\) (c’est-à-dire un champ scalaire), et un champ de vecteurs \(V\), alors la dérivée de \(f\) dans la direction \(V\) (notée \(\nabla_V f\)) est par définition égale à:
\[\begin{align}\nabla_V f &= V(f)\\ &=V^\alpha \frac{\partial f}{\partial x^\alpha} \end{align}\](en utilisant la convention de sommation d’Einstein, et en ne précisant pas le point \(p\), pour alléger la notation).
L’idée de la connexion affine est de généraliser cette notion de dérivée directionnelle à un champ de vecteurs, et plus seulement à un champ scalaire. Une connexion (affine) est une application notée \(\nabla\) (nabla), qui à deux champs de vecteurs \(U\) et \(V\) associe un champ de vecteurs \(\nabla_V U\), appelé la dérivée de \(U\) dans la direction \(V\). Pour être une connexion, l’application \(\nabla\) doit vérifier un certain nombre de propriétés caractéristiques d’une opération de dérivation (comme la linéarité ou la règle de Leibniz pour la dérivée d’un produit).
Si on représente \(U\) et \(V\) par leurs coordonnées dans la base \((e_\alpha) = \left(\frac{\partial}{\partial x^\alpha}\right)\), alors on montre que les coordonnées de la dérivée dans la même base sont de la forme:
\[(\nabla_V U)^\alpha = V^\mu \frac{\partial U^\alpha}{\partial x^\mu} + \Gamma^\alpha_{\mu\nu}V^\mu U^\nu\]On reconnait dans le premier terme la dérivée du champ scalaire \(U^\alpha\) dans la direction \(V\), et on voit apparaître un second terme faisant intervenir des coefficients \(\Gamma^\alpha_{\mu\nu}\) appelés coefficients de la connexion. Attention, dans ce second terme il y a deux indices répétés deux fois (\(\mu\) et \(\nu\)), donc avec la convention de sommation d’Einstein on a en fait une double somme:
\[\Gamma^\alpha_{\mu\nu}V^\mu U^\nu = \sum_{\mu=0}^{n-1}\sum_{\nu=0}^{n-1}\Gamma^\alpha_{\mu\nu}V^\mu U^\nu\]On peut noter que chaque coefficient de la connexion est en fait une fonction sur la variété (car sa valeur est a priori différente en chaque point), et que dans une variété de dimension 4, il y en a en tout \(4^3=64\) !
Les coefficients de la connexion ne sont rien d’autre que les coordonnées de la dérivée de chaque vecteur de base dans la direction des autres vecteurs de base, c’est-à-dire:
\[\Gamma^\alpha_{\mu\nu} = \left(\nabla_{e_\mu} e_\nu\right)^\alpha\]Mais à ce stade, rien ne nous permet de déterminer la valeur des coefficients de la connexion, qui dépend de la forme de la variété. On verra plus loin comment calculer ces coefficients à partir d’une métrique, mais chaque chose en son temps.
Pour comprendre la signification physique de la dérivée covariante, on peut reprendre l’exemple de la trajectoire d’un avion volant en ligne droite (on définira plus loin ce qu’est exactement une “ligne droite”). Si on choisit une carte ayant pour coordonnées la longitude et la latitude, la représentation de la trajectoire sur cette carte sera un général une courbe. Si on représente l’évolution des vecteurs de base le long de la trajectoire, on voit que ces vecteurs tournent par rapport à la courbe (dans le sens anti-horaire sur le schéma):
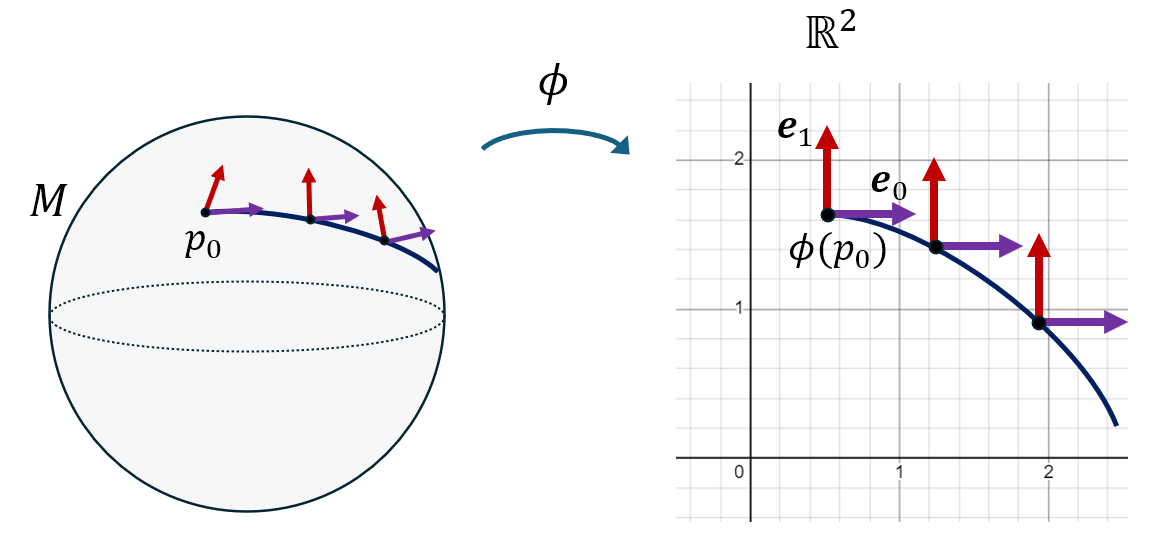
Si on suppose qu’au point \(p_0\) la latitude est de 45° et le vecteur tangent à la courbe est \(e_0\) (c’est-à-dire que l’avion vole initialement vers l’est), alors on peut calculer que les dérivées des vecteurs de base dans la direction \(e_0\) (donc en suivant la trajectoire) sont \(\nabla_{e_0}e_0 = \frac{1}{2}e_1\) et \(\nabla_{e_0}e_1 = -e_0\), ce qui traduit bien la rotation des vecteurs \(e_0\) et \(e_1\).
Transport parallèle et géodésiques
Un cas particulier important de dérivée covariante est celui où la dérivée d’un champ vecteur \(U\) est nulle le long d’une courbe \(\gamma\), c’est-à-dire dans la direction de ses vecteurs tangents en chaque point. Si on note \(\dot\gamma(\lambda)\) le vecteur tangent à la courbe au point \(\gamma(\lambda)\), on a donc:
\[\nabla_{\dot\gamma} U = 0\]On dit alors que le champ de vecteurs \(U\) est transporté parallèlement le long de la courbe \(\gamma\).
Le transport parallèle permet de retrouver une sorte de notion d’“égalité” entre vecteurs, mais uniquement de proche en proche. On peut aussi voir le transport parallèle comme l’équivalent d’une translation dans un espace affine. Attention, le transport parallèle dépend du trajet suivi, autrement dit si on transporte le même vecteur d’un point à un autre le long de deux courbes différentes, on obtient en général deux vecteurs différents au point d’arrivée:
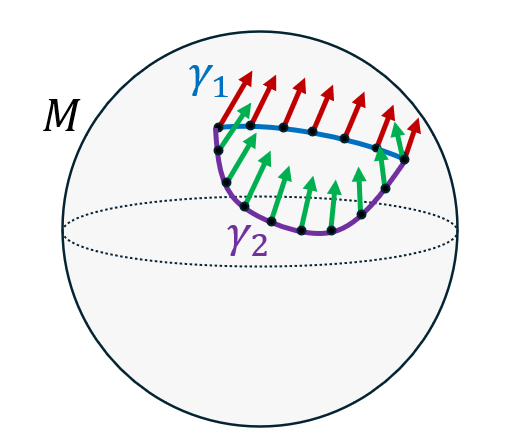
Le fait que le transport parallèle dépende de la trajectoire est précisément ce qui caractérise un espace courbe, car dans un espace affine (plat), la notion d’égalité entre vecteurs est définie de façon absolue, indépendamment de la trajectoire suivie.
On peut maintenant définir une géodésique comme une courbe \(\gamma\) dont les vecteurs tangents sont transportés parallèlement par la courbe elle-même, c’est-à-dire:
\[\nabla_{\dot\gamma} \dot\gamma = 0\]Pour faire le lien avec la physique, une géodésique représente la trajectoire d’un corps qui se déplace à vitesse “constante”, c’est-à-dire d’un corps libre (soumis à aucune force). Une géodésique sur une variété est donc l’équivalent d’une ligne droite dans un espace affine. Si on prend l’exemple d’une sphère, les géodésiques sont les trajectoires qui suivent les grands cercles, c’est-à-dire les cercles dont le centre est celui de la sphère (comme l’équateur ou les méridiens sur la Terre):
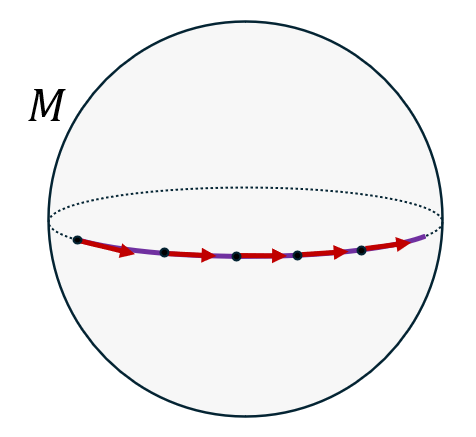
Si on note \(x^\alpha(\lambda)\) les coordonnées de la courbe dans une certaine carte, on peut alors montrer qu’une géodésique vérifie l’équation suivante:
\[\ddot{x}^\alpha + \Gamma_{\mu \nu}^\alpha \dot{x}^\mu \dot{x}^\nu = 0\]A SUIVRE dans la 3ème partie: tenseurs, métrique, connexion de Levi-Civita, courbure, équation d’Einstein